
 )(0≤x≤
)(0≤x≤ )与坐标轴围成的面积是________.
)与坐标轴围成的面积是________.
 )展开,得当0<x<
)展开,得当0<x< 时,函数值为负数;当
时,函数值为负数;当 <x<
<x< 时,函数值为负数.因此所求图形的面积为函数y=-sin(x-
时,函数值为负数.因此所求图形的面积为函数y=-sin(x- )在区间[0,
)在区间[0, ]上的积分值,加上y=sin(x-
]上的积分值,加上y=sin(x- )在区间[
)在区间[ ,
, ]上的积分值所得的和.最后根据积分的计算公式和运算法则加以计算,可得所求图形的面积.
]上的积分值所得的和.最后根据积分的计算公式和运算法则加以计算,可得所求图形的面积. )=sinxcos
)=sinxcos -cosxsin
-cosxsin =
= (sinx-cosx)
(sinx-cosx)
 时,sinx<cosx,函数值为负数;
时,sinx<cosx,函数值为负数; <x<
<x< 时,sinx>cosx,函数值为正数.
时,sinx>cosx,函数值为正数. [-sin(x-
[-sin(x- )]dx+
)]dx+ sin(x-
sin(x- )dx
)dx [
[ (-sinx+cosx)dx+
(-sinx+cosx)dx+ (sinx-cosx)]dx
(sinx-cosx)]dx [(cosx+sinx)
[(cosx+sinx)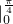 +(-cosx-sinx)
+(-cosx-sinx)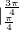 ]
] [(
[( )-(-
)-(- )]=
)]=



 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 8 |
| 5π |
| 4 |
| π |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com