
试写出一个求解下面二元一次方程组的算法.

|
解:对于二元一次方程组 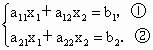 有 有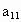 , ,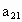 不同时为零时算法步骤如下: 不同时为零时算法步骤如下:
(1) 假定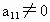 (若 (若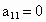 ,可将第一个方程与第二个方程互换), ,可将第一个方程与第二个方程互换),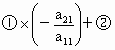 ,得 ,得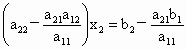 ,即方程组化为 ,即方程组化为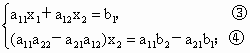
(2) 如果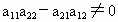 ,解方程④得 ,解方程④得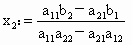 ;⑤ ;⑤
(3) 将⑤代入③,得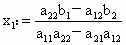 ;⑥ ;⑥
(4) 输出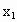 , ,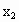 . .
如果 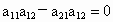 ,则由④可知,方程组无解或有无穷多组解. ,则由④可知,方程组无解或有无穷多组解.
( 注:本题中的符号“:=”是赋值符号,表示把符号后面表达式的值赋予前面自变量,以下同)通过本例可以发现,一个算法的设计要借助于一般问题的求解方法,同时又要全面考虑,把问题涉及的各种情形都要在算法中涉及到. |
|
求解二元一次方程组的方法通常有加减消元法(即高斯消去法)和公式法,结合这些方法我们便可以设计求解二元一次方程组的算法. |


科目:高中数学 来源: 题型:
| x2 |
| 25 |
| y2 |
| 9 |
| 2 |
| 5 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二下学期第一次月考理科数学试卷(解析版) 题型:解答题
(本小题满分14分)
(1) 证明:当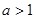 时,不等式
时,不等式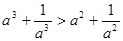 成立;
成立;
(2) 要使上述不等式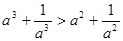 成立,能否将条件“
成立,能否将条件“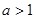 ”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
(3)请你根据⑴、⑵的证明,试写出一个类似的更为一般的结论,且给予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
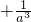 >a2
>a2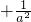 成立.
成立.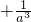 >a2
>a2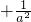 成立,能否将条件“a>1”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由.
成立,能否将条件“a>1”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com