
如果满足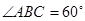 ,
,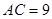 ,
,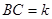 的△ABC恰有一个,那么
的△ABC恰有一个,那么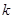 的取值范围是 ;
的取值范围是 ;
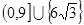
【解析】
试题分析:要对三角形解得各种情况进行讨论即:无解、有1个解、有2个解,从中得出恰有一个解时k满足的条件.根据题意,由于满足 ,
,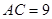 ,
, 的△ABC恰有一个,则可知解:(1)当AC<BCsin∠ABC,即9<ksin60°,即k>6
的△ABC恰有一个,则可知解:(1)当AC<BCsin∠ABC,即9<ksin60°,即k>6 时,三角形无解;(2)当AC=BCsin∠ABC,即12=ksin60°,即k=6
时,三角形无解;(2)当AC=BCsin∠ABC,即12=ksin60°,即k=6 时,三角形有1解;(3)当AC<BCsin∠ABC<BC,即ksin60°<9<k,即9<k<6
时,三角形有1解;(3)当AC<BCsin∠ABC<BC,即ksin60°<9<k,即9<k<6 ,三角形有2个解;(4)当0<BC≤AC,即0<k≤9时,三角形有1个解.综上所述:当0<k≤9或k=6
,三角形有2个解;(4)当0<BC≤AC,即0<k≤9时,三角形有1个解.综上所述:当0<k≤9或k=6 时,三角形恰有一个解.故答案为
时,三角形恰有一个解.故答案为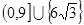
考点:解三角形
点评:本题属于解三角形的题型,主要考查了三角形解个数的问题,重在分情况分类讨论.易错点在于可能漏掉 k情况.


科目:高中数学 来源: 题型:
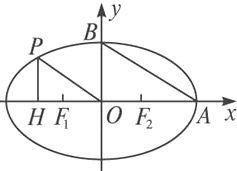 如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.
如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com