
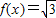 sin(ωx-
sin(ωx- )-cos(ωx-
)-cos(ωx- )(ω>0)图象的两相邻对称轴间的距离为
)(ω>0)图象的两相邻对称轴间的距离为 .
. )的值;
)的值; 个单位后,得到函数y=g(x)图象,求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求g(x)在区间[0, ]上的单调性.
]上的单调性.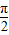 ,求出函数的周期,求出ω然后,直接求f(
,求出函数的周期,求出ω然后,直接求f(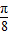 )的值;
)的值;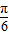 个单位后,得到函数y=g(x)图象,求出函数的解析式.然后求出函数的单调区间,即可求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求出函数的解析式.然后求出函数的单调区间,即可求g(x)在区间[0,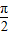 ]上的单调性.
]上的单调性.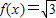 sin(ωx-
sin(ωx-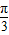 )-cos(ωx-
)-cos(ωx- )
) -
-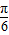 )=2sin(ωx-
)=2sin(ωx- )=-2cos(ωx)…(3分)
)=-2cos(ωx)…(3分)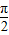 .
.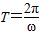 ,所以ω=2,∴f(x)=-2cos2x,f(
,所以ω=2,∴f(x)=-2cos2x,f(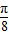 )=-
)=-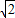 …(6分)
…(6分)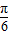 个单位后,得到函数y=g(x)图象,
个单位后,得到函数y=g(x)图象,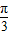 ),
),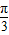 ≤2kπ,k∈Z,解得kπ
≤2kπ,k∈Z,解得kπ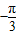 ≤x≤kπ
≤x≤kπ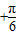 ,k∈Z
,k∈Z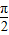 ]
]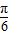 ]上递减,在[
]上递减,在[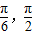 ]上递增…(13分)
]上递增…(13分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
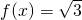 sin(ωx-
sin(ωx- )-cos(ωx-
)-cos(ωx- )(ω>0)图象的两相邻对称轴间的距离为
)(ω>0)图象的两相邻对称轴间的距离为 .
. )的值;
)的值; 个单位后,得到函数y=g(x)图象,求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求g(x)在区间[0, ]上的单调性.
]上的单调性.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
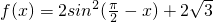 sin(π-x)cosx,
sin(π-x)cosx, 上的值域;
上的值域;查看答案和解析>>
科目:高中数学 来源:重庆市月考题 题型:解答题
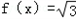 sin(
sin(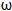 x﹣
x﹣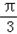 )﹣cos(
)﹣cos(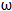 x﹣
x﹣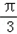 )(
)(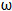 >0)图象的两相邻对称轴间的距离为
>0)图象的两相邻对称轴间的距离为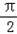 .
. 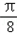 )的值;
)的值;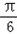 个单位后,得到函数y=g(x)图象,求g(x)在区间[0,
个单位后,得到函数y=g(x)图象,求g(x)在区间[0,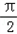 ]上的单调性.
]上的单调性.查看答案和解析>>
科目:高中数学 来源:2010-2011学年吉林省长春十一中高一(下)期中数学试卷(理科)(解析版) 题型:解答题
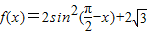 sin(π-x)cosx,
sin(π-x)cosx,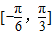 上的值域;
上的值域;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com