
设a为实数, 函数f(x)=x3-x2-x+a.
(1)求f(x)的极值;
(2)若曲线y=f(x)与x轴仅有一个交点, 求a的取值范围.
(1)f(x)的极大值是f( )=
)= ,极小值是f(1)=a-1.
,极小值是f(1)=a-1.
(2)当 时,曲线y=f(x)与x轴仅有一个交点.
时,曲线y=f(x)与x轴仅有一个交点.
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)因为a为实数, 函数f(x)=x3-x2-x+a.求解导数,结合导数的符号判定单调性得到
f(x)的极值;
(2)因为曲线y=f(x)与x轴仅有一个交点, 由此可知x取足够大的正数时有f(x)>0, x取足够小的负数时有f(x)<0.
所以曲线y=f(x)与x轴至少有一个交点,结合导数的思想判定得到。
(1) =3x2-2x-1.若
=3x2-2x-1.若 =0,则x=-
=0,则x=- 或x=1 ………… 2分
或x=1 ………… 2分
当x变化时, 、f(x)的变化情况如下表:
、f(x)的变化情况如下表:
|
|
|
|
|
1 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
f(x) |
|
极大值 |
|
极小值 |
|
…………4分
所以f(x)的极大值是f( )=
)= ,极小值是f(1)=a-1.………… 6分
,极小值是f(1)=a-1.………… 6分
(2)函数f(x)=x3-x2-x+a=(x-1)2(x+1)+a-1.
由此可知x取足够大的正数时有f(x)>0, x取足够小的负数时有f(x)<0.
所以曲线y=f(x)与x轴至少有一个交点. …………8分
结合f(x)的单调性可知,
当f(x)的极大值 <0,即a
<0,即a
 时,它的极小值也小于0.
时,它的极小值也小于0.
因此曲线y=f(x)与x轴仅有一个交点,它在(1,+ )上.
)上.
当f(x)的极小值a-1>0,即a
 时,它的极大值也大于0.
时,它的极大值也大于0.
因此曲线y=f(x)与x轴仅有一个交点,它在( )上.
)上.
所以当 时,曲线y=f(x)与x轴仅有一个交点.…… 12分
时,曲线y=f(x)与x轴仅有一个交点.…… 12分


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源:黄冈重点作业·高三数学(下) 题型:044
设a为实数,f(x)=a- (x∈R).
(x∈R).
(1)证明对于任意的实数a,f(x)在R上是增函数;
(2)试确定a的值,使f(x)为奇函数;
(3)当f(x)是奇函数时,对于给定的正实数k,解不等式:f-1(x)>log2![]() .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年辽宁沈阳实验中学北校高三12月月考文科数学试卷(解析版) 题型:填空题
设a为实数,函数f(x)=x3+ax2+(a-3)x的导函数为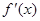 ,且
,且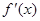 是偶函数, 则曲线:y=f(x)在点(2,f(2))处的切线方程为
.
是偶函数, 则曲线:y=f(x)在点(2,f(2))处的切线方程为
.
查看答案和解析>>
科目:高中数学 来源:2010年河北省高二第二学期期末考试数学(文)试卷 题型:解答题
(本小题满分12分)
设a为实数,函数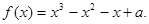
(Ⅰ)求f(x)的极值;
(Ⅱ)当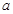 在什么范围内取值时,曲线y= f(x)与x轴仅有一个交点。
在什么范围内取值时,曲线y= f(x)与x轴仅有一个交点。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com