【答案】
分析:我们利用待定系数法求满足条件的复数Z,设=a+bi(a,b∈R)后,根据z=4i-zi,结合复数相等的充要条件,我们可以构造一个关于a,b的方程组,解方程组,即可得到满足条件的复数Z.
解答:解:设Z=a+bi(a,b∈R)
则∵z=4i-zi
∴a+bi=4i-(a+bi)i
∴a+bi=b+(4-a)i
∴
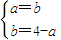
解得:
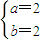
∴Z=2+i
故答案:2+i
点评:本题考查的知识点是复数代数形式的乘除运算,及复数相等的充要条件,其中根据复数相等的充要条件,构造一个关于a,b的方程组是解答本题的关键.
