
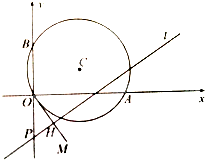 如图,已知点A(
如图,已知点A( ,0),B(0,1),圆C是以AB为直径的圆,直线l:
,0),B(0,1),圆C是以AB为直径的圆,直线l: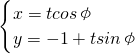 ,(t为参数).
,(t为参数). =3
=3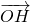 ,当φ变化时,求点M轨迹的参数方程,并指出它是什么曲线.
,当φ变化时,求点M轨迹的参数方程,并指出它是什么曲线. ,0),B(0,1),圆C是以AB为直径的圆,故点C的坐标为(
,0),B(0,1),圆C是以AB为直径的圆,故点C的坐标为( ,
, ),半径等于
),半径等于  |AB|=1,
|AB|=1, +
+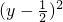 =1. (2’)
=1. (2’)
 ,在圆上任意取一点M(ρ,θ),则 ρ=2•cos(θ-
,在圆上任意取一点M(ρ,θ),则 ρ=2•cos(θ- ),
), ). (4’)
). (4’)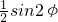 ,-
,- -
- cos2φ). (7’)
cos2φ). (7’) =3
=3 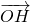 ,∴M(
,∴M(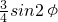 ,-
,- -
-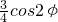 ),(9’)
),(9’)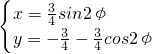 ,φ为参数,图形为圆. (10’)
,φ为参数,图形为圆. (10’) +
+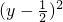 =1,由于OC和x轴的正方向的夹角为
=1,由于OC和x轴的正方向的夹角为 ,在圆上任意取一点M(ρ,θ),则 ρ=2•cos(θ-
,在圆上任意取一点M(ρ,θ),则 ρ=2•cos(θ- )即为所求.
)即为所求. =3
=3 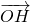 ,可得 M(
,可得 M(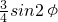 ,-
,- -
-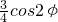 ),由此得到点M轨迹的参数方程.
),由此得到点M轨迹的参数方程.

科目:高中数学 来源: 题型:
(1)求动点Q的轨迹方程;
(2)设过点A的直线与点Q的轨迹交于E、F两点,A′(4a,0),求直线A′E、A ′F的斜率之和.
查看答案和解析>>
科目:高中数学 来源:2012年黑龙江省哈尔滨九中高考数学三模试卷(理科)(解析版) 题型:解答题
 ,0),B(0,1),圆C是以AB为直径的圆,直线l:
,0),B(0,1),圆C是以AB为直径的圆,直线l: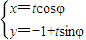 ,(t为参数).
,(t为参数).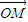 =3
=3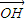 ,当φ变化时,求点M轨迹的参数方程,并指出它是什么曲线.
,当φ变化时,求点M轨迹的参数方程,并指出它是什么曲线.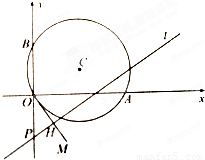
查看答案和解析>>
科目:高中数学 来源:2012年黑龙江省哈尔滨九中高考数学三模试卷(文科)(解析版) 题型:解答题
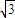 ,0),B(0,1),圆C是以AB为直径的圆,直线l:
,0),B(0,1),圆C是以AB为直径的圆,直线l: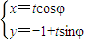 ,(t为参数).
,(t为参数).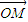 =3
=3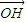 ,当φ变化时,求点M轨迹的参数方程,并指出它是什么曲线.
,当φ变化时,求点M轨迹的参数方程,并指出它是什么曲线.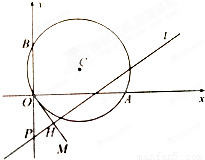
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com