
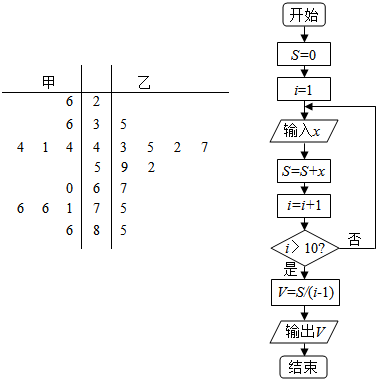
 为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.
为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.分析 (1)根据茎叶图中的数据,计算出对应的频率即可得到结论.
(2)根据程序框图,得到V为数据的平均数,根据平均数公式进行计算即可.
(3)根据茎叶图中数据的分布进行判断即可.
解答 解:(1)甲网站9月份共有10个数据,点击量少于50万次的有44,41,44,36,26,共5次,
则对应的概率P=$\frac{5}{10}=\frac{1}{2}$.
(2)由程序框图可知,程序的功能是计算平均值,
即V=$\frac{1}{10}$(43+45+42+47+59+52+67+75+85)=$\frac{463}{10}$=46.3,
即乙在9月份的平均点击量为46.3万次.
(3)甲网站的点击量比较分散,乙网站的点击量比较集中,故乙网站的关注度更稳定.
点评 本题考查了茎叶图,根据新高考服务于新教材的原则,作为新教材的新增内容--“茎叶”图是新高考的重要考点,茎叶图的茎是高位,叶是低位,这一点一定要注意.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
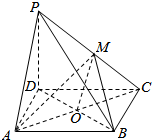 如图,已知P为平行四边形ABCD所在平面外一点,M是线段PC的中点.
如图,已知P为平行四边形ABCD所在平面外一点,M是线段PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 共面 | B. | 不共面 | C. | 共线 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com