
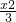 +y2≤1分成若干块,现用5种颜色给这若干块涂色,每块只涂一种颜色,任意两块不同色,共有120不同涂法,则t的取值范围是
+y2≤1分成若干块,现用5种颜色给这若干块涂色,每块只涂一种颜色,任意两块不同色,共有120不同涂法,则t的取值范围是 ,
, )
) ,
, )
) ,-
,- )∪(
)∪( ,
, )
) )(-
)(- ,+∞)
,+∞) +y2≤1可能分成2、3、4块,用5种颜色给这若干块涂色,每块只涂一种颜色,任意两块不同色,共有120不同涂法,说明共分成了4块,再数形结合得到t的范围
+y2≤1可能分成2、3、4块,用5种颜色给这若干块涂色,每块只涂一种颜色,任意两块不同色,共有120不同涂法,说明共分成了4块,再数形结合得到t的范围 +y2=1得
+y2=1得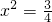 ,即x=±
,即x=±
 +y2≤1分成两部分,则涂色共有A52=20种,不合题意
+y2≤1分成两部分,则涂色共有A52=20种,不合题意 +y2≤1分成三部分,则涂色共有A53=60种,不合题意
+y2≤1分成三部分,则涂色共有A53=60种,不合题意 +y2≤1分成四部分,则涂色共有A54=120种,符合题意
+y2≤1分成四部分,则涂色共有A54=120种,符合题意 +y2≤1分成四部分,t的范围为(-
+y2≤1分成四部分,t的范围为(- ,
, )
)

 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
| x2-4x+m |
| x-2 |
| a |
| x |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:虹口区二模 题型:单选题
| x2 |
| 3 |
A.(-
| B.(-
| ||||||||||||||||
C.(-
| D.(-∞,
|
查看答案和解析>>
科目:高中数学 来源:2008年上海市虹口区高考数学二模试卷(文理合卷)(解析版) 题型:选择题
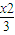 +y2≤1分成若干块,现用5种颜色给这若干块涂色,每块只涂一种颜色,任意两块不同色,共有120不同涂法,则t的取值范围是( )
+y2≤1分成若干块,现用5种颜色给这若干块涂色,每块只涂一种颜色,任意两块不同色,共有120不同涂法,则t的取值范围是( )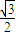 ,
,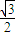 )
)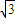 ,
, )
)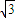 ,-
,- )∪(
)∪( ,
,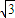 )
)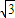 )(-
)(-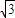 ,+∞)
,+∞)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com