解:(Ⅰ)由题意知P
1(-1,0)(1分)
∴a
1=-1,b
1=0(2分)
∴a
n=a
1+(n-1)•1=-1+n-1=n-2
∴b
n=2a
n+2=2(n-2)+2=2n-2
(Ⅱ)若k为奇数,
则f(k)=a
k=k-2f(k+5)=b
k+5=2k+8∴2k+8=2(k-2)-5无解(6分)
若k为偶数,
则f(k)=2k-2,f(k+5)=k+3∴k+3=2(2k-2)-5,解得k=4(8分)
综上,存在k=4使f(k+5)=2f(k)-5成立.(9分)
(Ⅲ)证明:
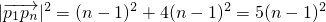
(1)当
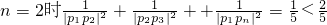
成立.(11分)
(2)当n≥3,n∈N
*时,
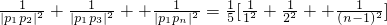
λx
12-2λx
1+λ-1=0.(12分)
=
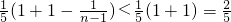
成立.(13分)
综上,当
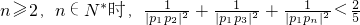
成立.(14分)
分析:(Ⅰ)由题意知P
1(-1,0),a
1=-1,b
1=0,由此可知a
n=n-2,b
n=2n-2.
(Ⅱ)若k为奇数,则f(k)=a
k=k-2f(k+5)=b
k+5=2k+8∴2k+8=2(k-2)-5无解.若k为偶数,则f(k)=2k-2,f(k+5)=k+3,由此可知存在k=4使f(k+5)=2f(k)-5成立.
(Ⅲ)
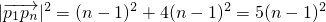
,由此入手能够证明,当
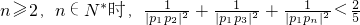
成立.
点评:本题考查数列的性质及其综合应用,解题时要认真审题,仔细解答.

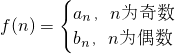 问是否存在k∈N*,使得f(k+5)=2f(k)-5成立?若存在,求出k的值,若不存在,说明理由;
问是否存在k∈N*,使得f(k+5)=2f(k)-5成立?若存在,求出k的值,若不存在,说明理由;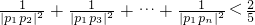 (n≥2,n∈N*).
(n≥2,n∈N*).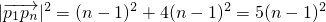
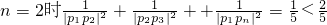 成立.(11分)
成立.(11分)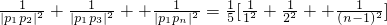 λx12-2λx1+λ-1=0.(12分)
λx12-2λx1+λ-1=0.(12分)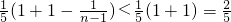 成立.(13分)
成立.(13分)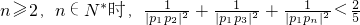 成立.(14分)
成立.(14分)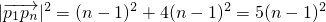 ,由此入手能够证明,当
,由此入手能够证明,当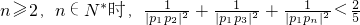 成立.
成立.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案