分析:(1)由题意知:a
n=2a
n-1+1,a
1=1,从而易得a
n+1=2(a
n-1+1),利用等比数列的通项公式可求得数列{a
n}的通项公式;
(2)由题意,a
1=1,b
1=1,S
1=0,当2≤n≤2014时,S
n=S
n-1+
,b
n=a
n•S
n,而S
n=S
1+
+
+…+
,从而可得
=
+
+…+
,
=
+
+…+
+
,于是易求
-
(n∈N
*,n≤2014)的值;
(3)由(2)知,知
=
,b
1=a
1=1,b
2=3,a
2=3,于是易求
| | (1+b1)(1+b2)…(1+bn) | | b1•b2…bn |
|
| |
=2(
+
+
+…+
),将所证的关系式转化为证明
+
+…+
+
<
即可,即证1+
+
+…+
<
,利用放缩法可证得结论.
解答:解:(1)由题意知:a
n=2a
n-1+1,a
1=1,
∴a
n+1=2(a
n-1+1),
∴a
n+1=(a
1+1)•2
n-1=2
n,
∴a
n=2
n-1(n∈N
*,n≤2014).
(2)由题意,a
1=1,b
1=1,S
1=0,
当2≤n≤2014时,S
n=S
n-1+
,b
n=a
n•S
n,
此时,S
n=S
1+
+
+…+
,
∴b
n=a
n(
+
+…+
),
∴
=
+
+…+
,
∴
=
+
+…+
+
,
∴
-
=
,
∴
-
=0,
当n=1时,
-
=
-
=-1,
综上,
-
=
;
(3)当n=1时,左=1+b
1=2,右=
b
1=
,
此时,1+b
1<
b
1,
当2≤n≤2014时,由(2)知
=
,
又b
1=a
1=1,b
2=3,a
2=3,
∴
| | (1+b1)(1+b2)…(1+bn) | | b1•b2…bn |
|
| |
=
•
•
…
•(1+b
n)
=
•
•
…
•(1+b
n)
=
•
•(1+b
n)
=2•(
+
)
=2(
+
+
+…+
)
即要证明的不等式转化为证明:
+
+…+
+
<
,
即证明1+
+
+…+
<
,
又a
n=2
n-1=4•2
n-2-1>3•2
n-2(n≥3),
∴1+
+
+…+
<1+
+
+
+…+
=1+
=1+
(1-
)<1+
=
.
∴(1+b
1)(1+b
2)…(1+b
n)<
b
1b
2…b
n.
综上,(1+b
1)(1+b
2)…(1+b
n)<
b
1b
2…b
n(n∈N
*,n≤2014)成立.
点评:本题考查数列的求和,着重考查数列的递推式的应用,考查程序框图的理解与应用,突出等价转化思想与抽象思维能力的考查,属于难题.

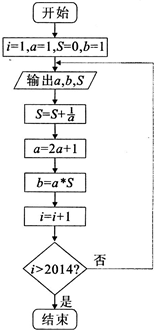 运行如图所示的程序框图,将输出的a依次记作a1,a2,…,an;输出的b依次记作b1,b2,…bn;输出的S依次记作S1,S2,…,Sn.(n∈N*)
运行如图所示的程序框图,将输出的a依次记作a1,a2,…,an;输出的b依次记作b1,b2,…bn;输出的S依次记作S1,S2,…,Sn.(n∈N*)
