
 ,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x-{x}.给出以下四个命题:
,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x-{x}.给出以下四个命题: 上单调递增;
上单调递增; 在[-2,2]上共有7个不相等的实数根.
在[-2,2]上共有7个不相等的实数根. ,x结合图象讨论四个命题的正确与否,由此可得本题的正确答案.
,x结合图象讨论四个命题的正确与否,由此可得本题的正确答案. <x
<x 时,满足不等式
时,满足不等式 的“亲密整数”m=0,
的“亲密整数”m=0, <x
<x 时,满足不等式
时,满足不等式 的“亲密整数”m=1,…,
的“亲密整数”m=1,…,
 上不是单调递增,因f(-
上不是单调递增,因f(- )=1,f(
)=1,f( )=1;故③错误;
)=1;故③错误; 在[-2,2]上共有7个不相等的实数根,正确.
在[-2,2]上共有7个不相等的实数根,正确.

 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:重庆市重庆一中2012届高三9月月考数学理科试题 题型:022
若整数m满足不等式 ,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)=x-{x}.给出以下四个命题:
,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)=x-{x}.给出以下四个命题:
①函数y=f(x),x∈R是周期函数且其最小正周期为1;
②函数y=f(x),x∈R的图象关于点(k,0),k∈Z中心对称;
③函数y=f(x),x∈R在[-![]() ,
,![]() ]上单调递增;
]上单调递增;
④方程f(x)=![]() sin(π,x)在[-2,2]上共有7个不相等的实数根.
sin(π,x)在[-2,2]上共有7个不相等的实数根.
其中正确命题的序号是________.(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
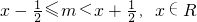 ,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x-{x}.给出以下四个命题:
,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x-{x}.给出以下四个命题: 上单调递增;
上单调递增;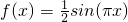 在[-2,2]上共有7个不相等的实数根.
在[-2,2]上共有7个不相等的实数根.查看答案和解析>>
科目:高中数学 来源:月考题 题型:填空题
 ,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x﹣{x}.给出以下四个命题:
,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x﹣{x}.给出以下四个命题: 上单调递增;
上单调递增; 在[﹣2,2]上共有7个不相等的实数根.
在[﹣2,2]上共有7个不相等的实数根.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com