
 的最大值为M,最小值为N,那么M+N=________.
的最大值为M,最小值为N,那么M+N=________.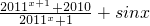 变形为f(x)=2011-
变形为f(x)=2011- +sinx,判断函数的单调性,根据函数在定义域上为增函数以及函数的定义域就可求出函数的最大值与最小值,进而求出最大值与最小值之和.
+sinx,判断函数的单调性,根据函数在定义域上为增函数以及函数的定义域就可求出函数的最大值与最小值,进而求出最大值与最小值之和.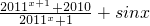 =
=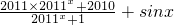 =
=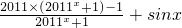
 +sinx
+sinx 上为增函数,∴y=
上为增函数,∴y= 在
在 上为减函数
上为减函数 在
在 上为增函数,
上为增函数, 上也为增函数
上也为增函数 +sinx在
+sinx在 上为增函数
上为增函数 ),N=f(-
),N=f(- )
) )+f(-
)+f(- )=4022-
)=4022-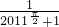 -
-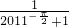 =4022-(
=4022-(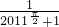 +
+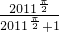 )=4021
)=4021

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| 1+tanx |
| 1-tanx |
| 1+f(x) |
| 1-f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| nπ |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市渝中区巴蜀中学高三(上)期中数学试卷(理科)(解析版) 题型:解答题
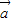 =(cosωx,2cosωx),
=(cosωx,2cosωx),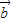 =(2cosωx,sinωx)(x∈R,ω>0),已知函数f(x)=
=(2cosωx,sinωx)(x∈R,ω>0),已知函数f(x)= +1的最小正周期是
+1的最小正周期是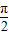 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com