
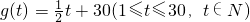 ,后20天价格为g(t)=45(31≤t≤50,t∈N).
,后20天价格为g(t)=45(31≤t≤50,t∈N).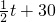 )=-t2+40t+6000,
)=-t2+40t+6000,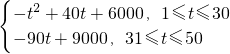 ;
;

科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
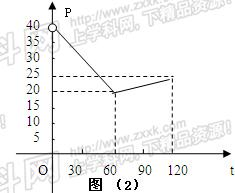
经市场调查,某种商品在过去50天的销售和价格均为销售时间t(天)的函数,且销售量近似地满足f (t) = – 2t + 200(1 ≤ t ≤ 50 , t ∈ N ),前30天价格为g (t) = ![]() t + 30 (1 ≤ t ≤ 30 , t ∈ N ),后20天价格为g (t) = 45 (31 ≤ t ≤ 50 , t ∈ N ).
t + 30 (1 ≤ t ≤ 30 , t ∈ N ),后20天价格为g (t) = 45 (31 ≤ t ≤ 50 , t ∈ N ).
(1)写出该种商品的日销售S与时间t的函数关系;
(2)求日销售S的最大值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济宁市邹城二中高一(上)期中数学试卷(解析版) 题型:解答题


查看答案和解析>>
科目:高中数学 来源:2010年福建省高二下学期期末考试(文科)数学卷 题型:解答题
(本小题满分12分)
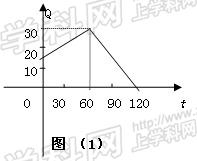
经市场调查,某种商品在过去50天的销售量和价格均为销售时间t(天)的函数,且销售量近拟地满足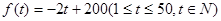 。前30天价格为
。前30天价格为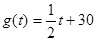
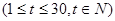 ,后20天价格为
,后20天价格为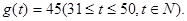
(1)写出该种商品的日销售额S与时间t的函数关系;
(2)求日销售额S的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com