
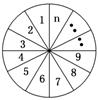
如图,将圆分成n个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.
(1)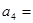 ;
;
(2)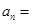 .
.
(1)18;(2) .
.
【解析】
试题分析:(1)设三种不同颜色分别为甲、乙、丙三种.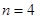 时,第1区域有3种选择,
第2区域有2种选择,第3区域有2种选择,因为第4区域要与第1区域颜色不同,故对第3区域的选择分类讨论:当第3区域与第1区域颜色相同时,第4区域有2种选择;当第3区域与第1区域颜色不同时,第4区域仅有1种选择.所以
时,第1区域有3种选择,
第2区域有2种选择,第3区域有2种选择,因为第4区域要与第1区域颜色不同,故对第3区域的选择分类讨论:当第3区域与第1区域颜色相同时,第4区域有2种选择;当第3区域与第1区域颜色不同时,第4区域仅有1种选择.所以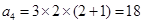 ;(2)当将圆分成n个区域,用3种不同颜色给每一个区域染色时,第1区域有3种染色方案,第2区域至第
;(2)当将圆分成n个区域,用3种不同颜色给每一个区域染色时,第1区域有3种染色方案,第2区域至第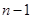 区域有2种染色方案.此时考虑第
区域有2种染色方案.此时考虑第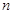 区域也有2种涂色方案,在此情况下有两种情况:
区域也有2种涂色方案,在此情况下有两种情况:
情况一:第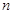 区域与第1区域同色,此时相当将这两区域重合,这时问题转化为3种不同颜色给圆上
区域与第1区域同色,此时相当将这两区域重合,这时问题转化为3种不同颜色给圆上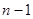 个区域涂色,即为
个区域涂色,即为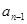 种染色方案;
种染色方案;
情况二:第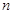 区域与第1区域不同色,此时问题就转化为用3种不同颜色给圆上
区域与第1区域不同色,此时问题就转化为用3种不同颜色给圆上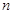 个区域染色,且相邻区域颜色互异,即此时的情况就是
个区域染色,且相邻区域颜色互异,即此时的情况就是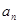 .根据分类原理可知
.根据分类原理可知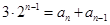 ,且满足初始条件:
,且满足初始条件: .
.
即递推公式为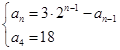 ,由
,由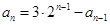 变形得
变形得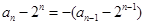 ,所以数列
,所以数列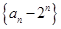 是以-1为公比的等比数列.所以
是以-1为公比的等比数列.所以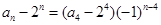 ,即
,即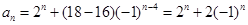 .当
.当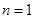 时,易知有3种染色方法,即
时,易知有3种染色方法,即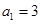 ,不满足上述通项公式;当
,不满足上述通项公式;当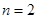 时,易知有
时,易知有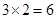 种染色方法,即
种染色方法,即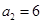 ,满足上述通项公式;当
,满足上述通项公式;当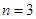 时,易知有
时,易知有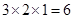 种染色方法,即
种染色方法,即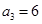 ,满足上述通项公式.
,满足上述通项公式.
综上所述,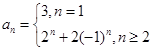 .
.
考点:数列的递推公式与通项公式、排列组合


科目:高中数学 来源: 题型:
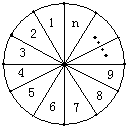 如图,将圆分成n个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.求
如图,将圆分成n个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.求查看答案和解析>>
科目:高中数学 来源: 题型:
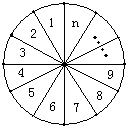
 如图,将圆分成n个区域,用3种不同颜色给每个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.
如图,将圆分成n个区域,用3种不同颜色给每个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.查看答案和解析>>
科目:高中数学 来源:重庆二模 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com