D
分析:根据命题p和q,分别得到命题
?p和
?q对应的不等式,分别解不等式得到
?p和
?q对应的x的取值范围.因为
?p是
?q的必要不充分条件,所以命题
?q对应的集合应该是命题
?p对应的集合的真子集,因此建立关于a的不等式组,解之可得实数a的取值范围.
解答:∵命题p:|4x-3|≤1,
∴命题
?p:|4x-3|>1,即4x-3<-1或4x-3>1
解之得
?p:x<

或x>1;
∵命题q:x
2-(2a+1)x+a
2+a≤0,
∴命题
?q:x
2-(2a+1)x+a
2+a>0,
即(x-a)[x-(a+1)]>0
解之得命题
?q:x<a或x>a+1;
∵
?p是
?q的必要不充分条件,
∴“
?q?
?p”成立且“
?p?
?q”不成立
因此,集合M={x|x<

或x>1},
集合N={x|x<a或x>a+1},且N是M的真子集,
∴

且等号不同时成立,
∴
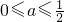
故选D
点评:本题以两个不等式的求解集的问题为载体,着重考查了充分必要条件的判断、集合包含关系的判断等知识点,属于基础题.


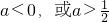
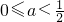
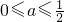
 或x>1;
或x>1; 或x>1},
或x>1}, 且等号不同时成立,
且等号不同时成立,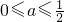


 阅读快车系列答案
阅读快车系列答案