
 +
+ ,数列{an}的前n项和为Tn.求证:Tn>2n-
,数列{an}的前n项和为Tn.求证:Tn>2n- .
. )(1+
)(1+ )…(1+
)…(1+ )≥a
)≥a 成立,求正数a的取值范围.
成立,求正数a的取值范围.
 ,代入可得an=
,代入可得an= +
+ =
= +
+ =2-(
=2-( -
- ),从而Tn=a1+a2+a3+…+an>2n-[(
),从而Tn=a1+a2+a3+…+an>2n-[( -
- )+(
)+( -
- )+…+(
)+…+( -
- )]=2n-(
)]=2n-(
 )>2n-
)>2n- ,于是结论即可证得.
,于是结论即可证得. ,可得bn=2n+1,则可得不等式(1+
,可得bn=2n+1,则可得不等式(1+ )(1+
)(1+ )…(1+
)…(1+ )≥a
)≥a ,分离系数a,可得a≤
,分离系数a,可得a≤ (1+
(1+ )(1+
)(1+ )…(1+
)…(1+ ),然后令f(n)=
),然后令f(n)= (1+
(1+ )(1+
)(1+ )…(1+
)…(1+ ),根据函数的单调性解决a的取值范围.
),根据函数的单调性解决a的取值范围.
 ,故xn-1=
,故xn-1= ,
, ,yn=
,yn= ,
, ,
, +
+ =
= +
+ =2-(
=2-( -
- ),
), <
< ,
, >
> ,
, -
- <
< -
- ,
, -
- )>2-(
)>2-( -
- ),
), -
- )+(
)+( -
- )+…+(
)+…+( -
- )]=2n-(
)]=2n-(
 )>2n-
)>2n- ,
, ,
, ,故bn=2n+1,
,故bn=2n+1, )(1+
)(1+ )…(1+
)…(1+ )≥a
)≥a ,
, (1+
(1+ )(1+
)(1+ )…(1+
)…(1+ )恒成立,
)恒成立, (1+
(1+ )(1+
)(1+ )…(1+
)…(1+ ),
), (1+
(1+ )(1+
)(1+ )…(1+
)…(1+ )(1+
)(1+ ),
), =
= •(1+
•(1+ )=
)= •
• =
= =
= >1,
>1, •
• =
= ,
, .
.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
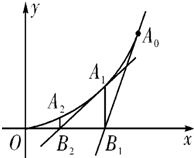 顶点在坐标原点,开口向上的抛物线经过A0(1,1),过A0作抛物 线的切线交x轴于B1,过B1点作x轴的垂线交抛物线于A1,过A1作抛物线的切线交x轴于B2,…,过An(xn,yn)作抛物线的切线交x轴于Bn+1(xn+1,0)
顶点在坐标原点,开口向上的抛物线经过A0(1,1),过A0作抛物 线的切线交x轴于B1,过B1点作x轴的垂线交抛物线于A1,过A1作抛物线的切线交x轴于B2,…,过An(xn,yn)作抛物线的切线交x轴于Bn+1(xn+1,0)| 1 |
| 1+xn |
| 1 |
| 1-xn+1 |
| 1 |
| 2 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 2n+3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省天门市部分重点中学联考高三(上)期中数学试卷(解析版) 题型:解答题
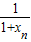 +
+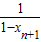 ,数列{an}的前n项和为Tn.求证:Tn>2n-
,数列{an}的前n项和为Tn.求证:Tn>2n- .
.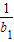 )(1+
)(1+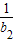 )…(1+
)…(1+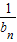 )≥a
)≥a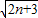 成立,求正数a的取值范围.
成立,求正数a的取值范围.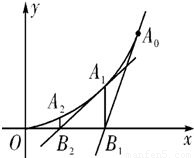
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第三次模拟考试理科数学试卷(解析版) 题型:解答题
顶点在坐标原点,开口向上的抛物线经过点 ,过点
,过点 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点 .
.

(1)求数列{ xn },{ yn}的通项公式 ;
;
(2)设 ,数列{ an}的前n项和为Tn.求证:
,数列{ an}的前n项和为Tn.求证: ;
;
(3)设 ,若对于任意正整数n,不等式
,若对于任意正整数n,不等式 …
… ≥
≥ 成立,求正数a的取值范围.
成立,求正数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省八市高三三月联考理科数学 题型:解答题
(本题满分14分)
顶点在坐标原点,开口向上的抛物线经过点 ,过点
,过点 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点 .
.
(I)求数列{ xn
},{ yn}的通项公式 ;
;
(II)设 ,数列{ an}的前n项和为Tn.求证:
,数列{ an}的前n项和为Tn.求证: ;
;
(III)设 ,若对于任意正整数n,不等式
,若对于任意正整数n,不等式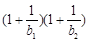 …
… ≥
≥ 成立,求正数a的取值范围.
成立,求正数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com