
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 某人要建造一间地面面积为24m2、墙高为3m,一面靠旧墙的矩形房屋.利用旧墙需维修,其它三面墙要新建,由于地理位置的限制,房子正面的长度x(单位:m)不得超过a(单位:m)(其平面示意图如图).已知旧墙的维修费用为150元/m2,新墙的造价为450元/m2,屋顶和地面的造价费用合计为5400元(不计门、窗的造价).
某人要建造一间地面面积为24m2、墙高为3m,一面靠旧墙的矩形房屋.利用旧墙需维修,其它三面墙要新建,由于地理位置的限制,房子正面的长度x(单位:m)不得超过a(单位:m)(其平面示意图如图).已知旧墙的维修费用为150元/m2,新墙的造价为450元/m2,屋顶和地面的造价费用合计为5400元(不计门、窗的造价).查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•宝坻区一模)某单位建造一间地面面积为12m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过a米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.
(2008•宝坻区一模)某单位建造一间地面面积为12m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过a米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.查看答案和解析>>
科目:高中数学 来源: 题型:
(1)把房屋总造价y表示成x的函数,并写出该函数的定义域.
(2)当侧面的长度x为多少时,总造价最低?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广西桂林中学高三上学期11月月考理科数学卷 题型:选择题
某单位建造一间地面面积为12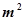 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度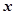 不得超过
不得超过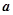 米,房屋正面的造价为400元
米,房屋正面的造价为400元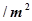 ,房屋侧面的造价为150元
,房屋侧面的造价为150元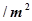 ,屋顶和底面的造价费用合计为5800元,如果墙高为3米.且不计房屋背面的费用.
,屋顶和底面的造价费用合计为5800元,如果墙高为3米.且不计房屋背面的费用.
(1)把房屋总造价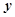 表示成
表示成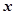 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(2)当侧面的长度为多少时,总造价最低?最低总造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com