
已知方程tan2x一 tan
x+1=0在x
tan
x+1=0在x [0,n
[0,n )( n
)( n N*)内所有根的和记为an
N*)内所有根的和记为an
(1)写出an的表达式;(不要求严格的证明)
(2)记Sn = a1 + a2 +…+ an求Sn;
(3)设bn =(kn一5)  ,若对任何n
,若对任何n N* 都有an
N* 都有an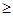 bn,求实数k的取值范围.
bn,求实数k的取值范围.
(1) 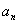 =(n2一
=(n2一 )
)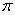 (2)
(2) 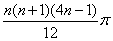 (3) k
(3) k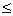 4
4
【解析】
试题分析:解:( 1)解方程得tanx=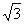 或
或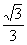 ,当n=1时,x=
,当n=1时,x=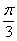 或
或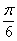 ,此时
,此时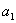 =
=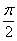 ,
,
当n=2时,x=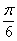 ,
,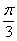 ,
,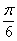 +
+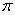 ,
,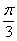 +
+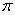 ,∴
,∴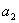 =
=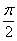 +(
+(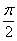 +2
+2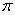 )
)
依次类推: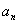 =
=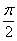 +(
+(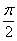 +2
+2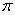 )+…+[
)+…+[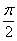 +2(n一1)
+2(n一1) 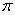 ],
],
∴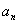 =(n2一
=(n2一 )
)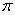
(2) 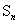 =(12 +22 +…+n2 )
=(12 +22 +…+n2 ) 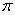 一
一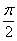 (1+2+…+n)
(1+2+…+n)
=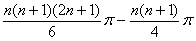
=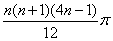
(3)由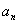
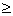
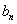 得(n2—
得(n2— )
)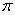
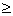 (kn一5)
(kn一5) 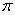 ,
,
∴kn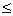 n2一
n2一 +5
∵n∈N*,∴k
+5
∵n∈N*,∴k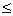 n+
n+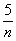 一
一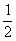 ,
,
设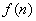 = n+
= n+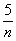 一
一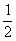 ,
,
易证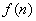 在(0,
在(0,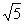 )上单调递减,在(
)上单调递减,在(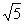 ,+∞)上单调递增
,+∞)上单调递增
∵n∈N*,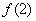 =4,
=4,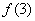 =4∴n=2,
=4∴n=2,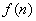 min =4,
min =4,
∴k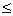 4
4
考点:数列的通项公式与前n项和
点评:解决的关键是利用数列的累加法来求解其通项公式,同时能利用分组求和来得到和式,属于基础题。


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com