
已知点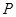 在曲线
在曲线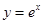 上,点
上,点 在曲线
在曲线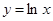 上,则
上,则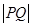 的最小值是
的最小值是
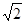
【解析】
试题分析:∵曲线y=ex(e自然对数的底数)与曲线y=lnx互为反函数,其图象关于y=x对称,则对于求解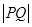 的最小值问题,故可先求点P到直线y=x的最近距离d,设曲线y=ex上斜率为1的切线为y=x+b,∵y′=ex,由ex=1,得x=0,故切点坐标为(0,1),即b=1,∴d=
的最小值问题,故可先求点P到直线y=x的最近距离d,设曲线y=ex上斜率为1的切线为y=x+b,∵y′=ex,由ex=1,得x=0,故切点坐标为(0,1),即b=1,∴d=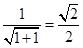 ,∴丨PQ丨的最小值为2d=
,∴丨PQ丨的最小值为2d=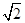 。
。
考点:本题主要考查了互为反函数的函数图象的对称性,导数的几何意义,曲线的切线方程的求法,转化化归的思想方法
点评:考虑到两曲线关于直线y=x对称,求丨PQ丨的最小值可转化为求P到直线y=x的最小距离,再利用导数的几何意义,求曲线上斜率为1的切线方程,从而得此距离。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014届河南郑州第四中学高二下学期期中考试理科数学试卷(解析版) 题型:选择题
已知点 在曲线
在曲线 上,
上, 为曲线在点
为曲线在点 处的切线的倾斜角,则
处的切线的倾斜角,则 取值范围是
取值范围是
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com