
已知数列 ,
,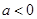 满足
满足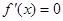 ,
,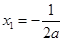 ,
,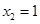 ,
,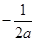 .
.
(1)求证:数列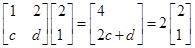 是等差数列,并求数列
是等差数列,并求数列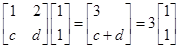 的通项公式;
的通项公式;
(2)设数列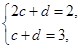 满足
满足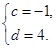 ,对于任意给定的正整数
,对于任意给定的正整数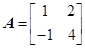 ,是否存在正整数
,是否存在正整数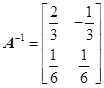 ,
,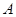 (
( ),使得
),使得 ,
, ,
, 成等差数列?若存在,试用
成等差数列?若存在,试用 表示
表示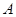 ,
, ;若不存在,说明理由.
;若不存在,说明理由.
(1)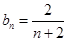 ,(2)当
,(2)当 时,不存在
时,不存在 ,
,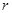 满足题设条件;当
满足题设条件;当 时,存在
时,存在 ,
, ,满足题设条件.
,满足题设条件.
解析试题分析:(1)求证数列 是等差数列,就是确定
是等差数列,就是确定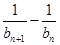 为一个常数.因此首先得到关于
为一个常数.因此首先得到关于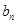 与
与 的关系式,因为
的关系式,因为 ,所以
,所以 ,则
,则 ,然后按提示,将所求关系式进行变形,即取倒数,得:
,然后按提示,将所求关系式进行变形,即取倒数,得: ,又
,又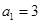 ,所以
,所以 ,故
,故 是首项为
是首项为 ,公差为
,公差为 的等差数列,即
的等差数列,即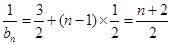 ,所以
,所以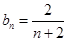 .(2)先明确数列
.(2)先明确数列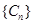 ,由(1)得
,由(1)得 ,所以
,所以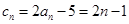 ,然后假设存在,得一等量关系:若
,然后假设存在,得一等量关系:若 ,
, ,
, 成等差数列,则
成等差数列,则 ,如何变形,是解题的关键,这直接影响解题方向.题中暗示,用p表示,所以由
,如何变形,是解题的关键,这直接影响解题方向.题中暗示,用p表示,所以由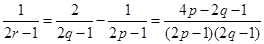 得:
得: .令
.令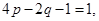 得
得 ,因为要
,因为要 ,所以分情况讨论,当
,所以分情况讨论,当 时,
时,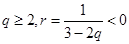 ,
, ,
, ,
, 成等差数列不成立.当
成等差数列不成立.当 时,
时, ,
, ,即
,即 .
.
试题解析:(1)因为 ,所以
,所以 ,
,
则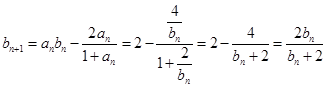 , 2分
, 2分
所以 ,
,
又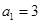 ,所以
,所以 ,故
,故 是首项为
是首项为 ,公差为
,公差为 的等差数列, 4分
的等差数列, 4分
即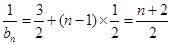 ,所以
,所以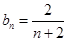 . 6分
. 6分
(2)由(1)知 ,所以
,所以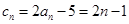 ,
,
①当 时,
时,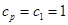 ,
,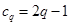 ,
,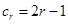 ,
,
若 ,
, ,
, 成等差数列,则
成等差数列,则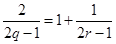 (
( ),
),
因为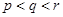 ,所以
,所以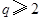 ,
, ,
,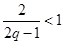 ,
, ,
,
所以( )不成立.
)不成立.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
(12分)(2011•重庆)设实数数列{an}的前n项和Sn满足Sn+1=an+1Sn(n∈N*).
(Ⅰ)若a1,S2,﹣2a2成等比数列,求S2和a3.
(Ⅱ)求证:对k≥3有0≤ak≤ .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•湖北)已知等比数列{an}满足:|a2﹣a3|=10,a1a2a3=125.
(1)求数列{an}的通项公式;
(2)是否存在正整数m,使得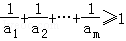 ?若存在,求m的最小值;若不存在,说明理由.
?若存在,求m的最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校餐厅每天供应500名学生用餐,每星期一有A, B两种菜可供选择。调查表明,凡是在这星期一选A菜的,下星期一会有 改选B菜;而选B菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有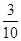 改选A菜。用
改选A菜。用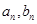 分别表示第
分别表示第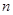 个星期选A的人数和选B的人数.
个星期选A的人数和选B的人数.
⑴试用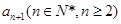 表示
表示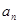 ,判断数列
,判断数列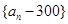 是否成等比数列并说明理由;
是否成等比数列并说明理由;
⑵若第一个星期一选A种菜的有200人,那么第10个星期一选A种菜的大约有多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若函数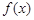 满足:集合
满足:集合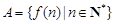 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数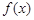 是等比源函数.
是等比源函数.
(1)判断下列函数:①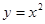 ;②
;②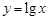 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(2)证明:函数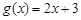 是等比源函数;
是等比源函数;
(3)判断函数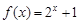 是否为等比源函数,并证明你的结论.
是否为等比源函数,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设数列{an}前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N*.
(1)求a1的值.
(2)求数列{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com