一束光线从点A(-2,1)出发经x轴反射到圆C:(x-2)2+(y-2)2=1上,光线的最短路程是 .
【答案】
分析:由圆C的方程找出圆心C的坐标及圆的半径r,找出C关于x轴的对称点C′,连接AC′,利用两点间的距离公式求出|AC′|的长,用|AC′|的长减去圆的半径,即可得到光线的最短路程.
解答:解:根据题意画出图形,如图所示:
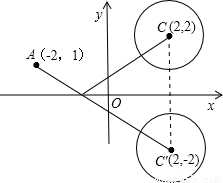
作出圆心C关于x的对称点C′,连接AC′,
由圆C:(x-2)
2+(y-2)
2=1,得到圆心C坐标为(2,2),圆的半径r=1,
可得C′的坐标为(2,-2),又A(-2,1),
∴|AC′|=
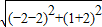
=5,
则光线的最短路程是|AC′|-r=5-1=4.
故答案为:4
点评:此题考查了对称的性质,两点间的距离公式,以及圆的标准方程,利用了数形结合的思想,解题的思路为根据题意画出图形,作出圆关于x轴的对称图形,利用两点之间线段最短可得出光线的最短距离.


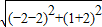 =5,
=5,

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案