
(07年湖北卷文)(12分)
如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,![]() .
.
(I)求证:平面![]() 平面
平面![]() ;
;
(II)试确定角![]() 的值,使得直线
的值,使得直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.

本小题主要考查线面关系、直线与平面所成角的有关知识,考查空间想象能力和推理运算能力以及应用向量知识解决数学问题的能力.
解析:解法1:(Ⅰ)![]() ,
,![]() 是等腰三角形,又
是等腰三角形,又![]() 是
是![]() 的中点,
的中点,
![]() ,又
,又![]() 底面
底面![]() .
.![]() .于是
.于是![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ) 过点![]() 在平面
在平面![]() 内作
内作![]() 于
于![]() ,则由(Ⅰ)知
,则由(Ⅰ)知![]() 平面
平面![]() .
.
连接![]() ,于是
,于是![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角.
所成的角.
依题意![]() ,所以
,所以
在![]() 中,
中,![]() ;
;
在![]() 中,
中,![]() ,
,
![]() .
.
![]() ,
,![]() .
.
故当![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
解法2:(Ⅰ)以![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
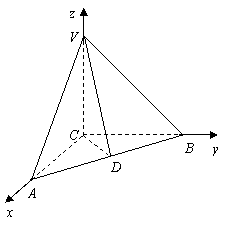
则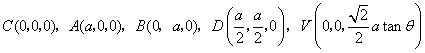 ,
,
于是, ,
,![]() ,
,![]() .
.
从而![]() ,即
,即![]() .
.
同理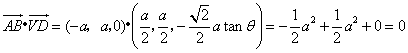 ,
,
即![]() .又
.又![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() .
.
![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由![]() .
.
得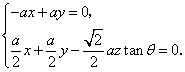
可取![]() ,又
,又![]() ,
,
于是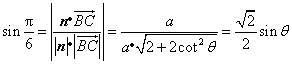 ,
,
即![]()
![]() ,
,![]() .
.
故交![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
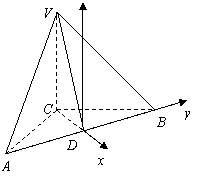
解法3:(Ⅰ)以点![]() 为原点,以
为原点,以![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
则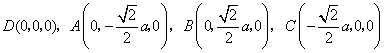 ,
,
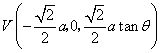 ,于是
,于是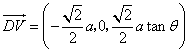 ,
,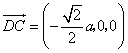 ,
,![]() .
.
从而![]()
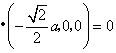 ,即
,即![]() .
.
同理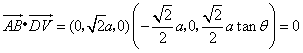 ,即
,即![]() .
.
又![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由![]() ,得
,得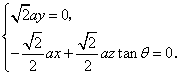
可取![]() ,又
,又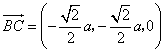 ,
,
于是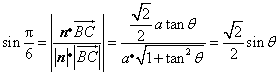 ,
,
即![]() .
.
故交![]() 时,
时,
即直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
(07年湖北卷文)为了了解学校学生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方图如图所示,根据此图,估计该校2000名高中男生中体重大于70.5公斤的人数为
A.300 B.350
C.420 D.450

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com