练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，在圆C中，若
    AB
    •
    AC
    =1，则弦AB的长度为
     
    ．
    考点：平面向量数量积的运算
    专题：平面向量及应用
    分析：设圆的半径为r，AB=2d，由数量积的定义得到
    AB
    •
    AC
    =1=2dr
    d
    r
    ，解得d即可．
    解答： 解：设圆的半径为r，AB=2d，所以
    AB
    •
    AC
    =1=2dr
    d
    r
    ，解得d=
    		2
    2
    ，所以AB=
    		2
    ；
    故答案为：
    		2
    ．
    点评：本题考查了向量的数量积以及圆的半径、弦长、弦心距的关系，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知两直角边长分别为a，b的直角三角形的面积大小与其周长大小相等，则ab的最小值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}中，a1=2，a2=1，
    2
    an
    =
    1
    an+1
    +
    1
    an-1
    （n≥2，n∈N*），其通项公式an=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=ax+
    1-x
    ax
    （a＞0）
    （1）利用函数单调性的定义，判断函数f（x）在（0，+∞）上的单调性；
    （2）求函数y=f（x）在（0，1]上的最小值g（a）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（t）=t+
    1
    t
    -
    3
    2
    ，t∈[
    1
    2
    ，2    ]．
    （1）求f（t）的值域G；
    （2）若对于G内的所有实数x，不等式-x2+x+2m2≥1恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知O是等边△ABC边AC（不含端点）上的一点，D为AB上的点，且|
    AB
    |=2|
    OD
    |=2，
    OA
    +
    OB
    =2
    OD
    ，则
    AO
    •
    OD
    =（　　）
    A、-
    1
    2
    B、
    1
    2
    C、-1
    D、1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=cosx，x∈（0，2π）有两个不同的零点x1，x2，且方程f（x）=m（m≠0）有两个不同的实根x3，x4，若把这四个数按从小到大排列构成等差数列，则实数m=（　　）
    A、
    1
    2
    B、-
    1
    2
    C、
    		3
    2
    D、-
    		3
    2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

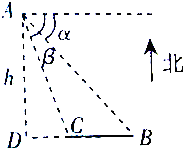    如图，从气球A测得正前方的济南全运会东荷、西柳两个场馆B、C的俯角分别为α、β，此时气球的高度为h，则两个场馆B、C间的距离为（　　）
    A、
    hsinαsinβ
    sin(α-β)
    B、
    hsin(β-α)
    sinαsinβ
    C、
    hsinα
    sinβsin(α-β)
    D、
    hsinβ
    sinαsin(α-β)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图过拋物线y2=2px（p＞0）的焦点F的直线依次交拋物线及准线于点A，B，C，若|BC|=2|BF|，且|AF|=3，则拋物线的方程为（　　）
    A、y2=
    3
    2
    x
    B、y2=3x
    C、y2=
    9
    2
    x
    D、y2=9x

    查看答案和解析>>

    同步练习册答案