
| 1 |
| 3 |
|
|
|
|
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| bk+1 |
| bk |
| k-n |
| ab+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年海拉尔二中阶段考试五理) 已知各项全不为零的数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,其中
,其中![]() .
.
(I)求数列![]() 的通项公式;
的通项公式;
(II)对任意给定的正整数![]() ,数列
,数列![]() 满足
满足![]()
![]()
(![]() ),
),![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省保定市高三上学期期末调研考试理科数学试卷(解析版) 题型:解答题
已知各项全不为零的数列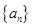 的前
的前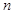 项和为
项和为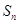 ,且
,且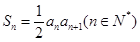 ,其中
,其中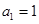
(1)
求数列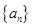 的通项公式;
的通项公式;
(2)在平面直角坐标系内,设点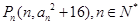 ,试求直线
,试求直线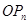 斜率的最小值(
斜率的最小值(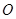 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(陕西) 题型:解答题
(本小题满分12分)
已知各项全不为零的数列{ak}的前k项和为Sk,且Sk= N*),其中a1=1.
N*),其中a1=1.
(Ⅰ)求数列{ak}的通项公式;
(Ⅱ)对任意给定的正整数n(n≥2),数列{bk}满足 (k=1,2,…,n-1),b1=1.
(k=1,2,…,n-1),b1=1.
求b1+b2+…+bn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com