
(12分)已知两点
 满足条件
满足条件 的动点P的轨迹是曲线
的动点P的轨迹是曲线 ,
, 与曲线
与曲线 交于
交于 、
、 两点.
两点.
(1)求k的取值范围;
(2)如果 求直线l的方程.
求直线l的方程.
科目:高中数学 来源: 题型:
(本小题满分12分)如图所示,已知圆![]()
|
足![]() 的轨迹为曲线E.
的轨迹为曲线E.
(1)求曲线E的方程;(II)若过定点F(0,2)
的直线交曲线E于不同的两点G、H(点G在点F、H之间),
且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁沈阳二中等重点中学协作体高三领航高考预测十二理数学卷(解析版) 题型:解答题
(本题满分为12分)
已知函数 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(1)求实数 的值;
的值;
(2)求 在区间
在区间 上的最大值;
上的最大值;
(3)对任意给定的正实数 ,曲线
,曲线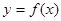 上是否存在两点
上是否存在两点 ,使得
,使得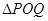 是以
是以 为直角顶点的直角三角形,且此三角形斜边的中点在轴上?请说明理由.
为直角顶点的直角三角形,且此三角形斜边的中点在轴上?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() (2,0)的直线与椭圆
(2,0)的直线与椭圆![]() 相交于两点
相交于两点![]() ,设
,设![]() 为椭圆上一点,且满
为椭圆上一点,且满![]() (O为坐标原点),当
(O为坐标原点),当![]() <
<![]() 时,求实数
时,求实数![]() 取值范围.
取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com