
分析 (1)利用已知条件,推出数列是等比数列,然后求解通项公式.
(2)利用函数关系式,求出数列{bn}是等差数列,然后求出通项公式.
(3)利用等差数列转化求解数列的和即可.
解答 解:(1)∵$\left\{\begin{array}{l}3{S_n}-5{S_n}_{-1}=3\\ 3{S_{n+1}}-5{S_n}=3\end{array}\right.(n≥2)$,两式相减得3an+1-5an=0,
又∴$\frac{{{a_{n+1}}}}{a_n}=\frac{5}{3}(n≥2)$,又当n=2时,3S2-5S1=3,
得${a_2}=\frac{5}{3}$,即$\frac{a_2}{a_1}=\frac{5}{3}$,∴$\frac{{{a_{n+1}}}}{a_n}=\frac{5}{3}(n≥1)$,
∴数列{an}为等比数列${a_n}={(\frac{5}{3})^{n-1}}$ …(4分)
(2)由已知得$f(x)=\frac{2x+3}{3x}$,∴${b_n}=f(\frac{1}{{{b_{n-1}}}})=\frac{{\frac{2}{{{b_{n-1}}}}+3}}{{\frac{3}{{{b_{n-1}}}}}}={b_{n-1}}+\frac{2}{3}(n≥2)$,
∴数列{bn}是以b1=1为首项,$\frac{2}{3}$为公差的等差数列.
∴${b_n}=\frac{2}{3}n+\frac{1}{3}$…(8分)
(3)Tn=(b1b2-b2b3)+(b3b4-b4b5)+…+(b2n-1b2n-b2nb2n+1)
=b2(b1-b3)+b4(b3-b5)+…+b2n(b2n-1-b2n+1)
=$-2d({b_2}+{b_4}+…+-{b_{2n}})=-2×\frac{2}{3}[{n×\frac{5}{3}+\frac{n(n-1)}{2}×\frac{4}{3}}]$=$-\frac{8}{9}{n^2}-\frac{4}{3}n$…(12分)
点评 本题考查数列的递推关系式以及数列与函数相结合,考查转化思想以及分析问题解决问题的能力.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -15 | B. | 15 | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{9\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
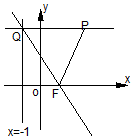 如图在直角坐标系xOy中,过动点P的直线与直线l:x=-1垂直,垂足为Q,点F(1,0)满足$\overrightarrow{FP}•\overrightarrow{FQ}=\overrightarrow{QP}•\overrightarrow{QF}$.
如图在直角坐标系xOy中,过动点P的直线与直线l:x=-1垂直,垂足为Q,点F(1,0)满足$\overrightarrow{FP}•\overrightarrow{FQ}=\overrightarrow{QP}•\overrightarrow{QF}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com