
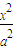 +
+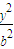 =1,a>b>0的左焦点为F1,上顶点为A,过点A与AF1垂直的直线分别交椭圆和x轴正半轴于P、Q两点,且P分向量
=1,a>b>0的左焦点为F1,上顶点为A,过点A与AF1垂直的直线分别交椭圆和x轴正半轴于P、Q两点,且P分向量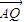 所成的比为λ.
所成的比为λ.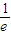 -e)2的取值范围;
-e)2的取值范围;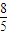 时,过A、Q、F1三点的圆恰好与直线L:x+
时,过A、Q、F1三点的圆恰好与直线L:x+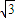 y+3=0相切,求椭圆的方程.
y+3=0相切,求椭圆的方程. 所成的比为λ,可得点P的坐标,代入椭圆方程,再利用
所成的比为λ,可得点P的坐标,代入椭圆方程,再利用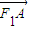 •
• =0,联立可表示出(
=0,联立可表示出(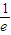 -e)2,进而根据λ∈(1,2),可探求椭圆离心率(
-e)2,进而根据λ∈(1,2),可探求椭圆离心率( -e)2的取值范围;
-e)2的取值范围;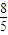 时,e-
时,e-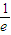 =-
=- ,故e=
,故e= ,a=2c.利用圆恰好与直线L:x+
,a=2c.利用圆恰好与直线L:x+ y+3=0相切,可求a=2,b=
y+3=0相切,可求a=2,b=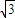 ,从而得到椭圆方程
,从而得到椭圆方程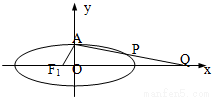 解:(1)设Q(x,0),F1(-c,0),A(0,b),
解:(1)设Q(x,0),F1(-c,0),A(0,b),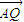 所成的比为λ,
所成的比为λ,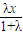 ,
, ),∴(
),∴(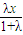 )2
)2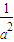 +(
+(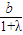 )2
)2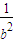 =1. ①
=1. ①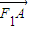 =(c,b),
=(c,b), =(x,-b),
=(x,-b),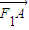 •
• =0,
=0, )2
)2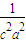 +(
+(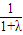 )2=1,
)2=1,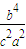 =(1+λ)2-1,即(
=(1+λ)2-1,即(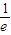 -e)2=1+
-e)2=1+ ∈(2,3).
∈(2,3). 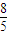 时,e-
时,e-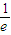 =-
=- ,
, ,a=2c.
,a=2c.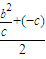 ,0)=(
,0)=(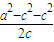 ,0)=(c,0),
,0)=(c,0),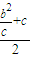 =
= =a.
=a. y+3=0相切,得
y+3=0相切,得 =a,
=a, .
.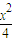 +
+ =1.
=1.

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源:2007年天津市高考数学试卷(理科)(解析版) 题型:解答题
 =1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
=1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为 .
. ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 +
+ =1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2.
=1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2. =λ1
=λ1 ,
,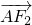 =λ2
=λ2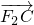 ,当A在椭圆上运动时,求证:λ1+λ2为定值.
,当A在椭圆上运动时,求证:λ1+λ2为定值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省九江市都昌二中高三(上)周考数学试卷(6)(文科)(解析版) 题型:解答题
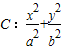 =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
•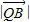 =
=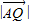 •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上.查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省哈尔滨九中高二(上)期末数学试卷(文科)(解析版) 题型:解答题
 =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
• =
= •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上.查看答案和解析>>
科目:高中数学 来源:2009年高考数学压轴试卷集锦(8)(解析版) 题型:解答题
 =1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P(
=1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P( ,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______
,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com