分析:(1)利用正弦定理列出关系式,将已知BC与B=2A代入,利用二倍角的正弦函数公式化简即可
的值;得出的值表示出AC,利用余弦函数的值域即可确定出AC的范围;
(2)所求式子利用二倍角的余弦函数公式化简,整理后再利用和差化积公式计算,求出A的度数,即可做出判断.
解答:解:(1)∵B=2A,
∴sinB=sin2A=2sinAcosA,且b=2a,
∴cosA=
=
,
∴
=
=
=2a=2BC=2,
∴AC=2cosA,
∵0<B=2A<90°,
∴0<A<45°,
∵0<C=180°-A-B=180°-3A<90°,
∴30°<A<45°,
∴
<cosA<
,即1<2cosA<
,
则AC范围为(1,
);
(2)将1+cos
2A=cos
2B+cos
2C,化简得:1+
=
+
,
整理得:1+cos2A=cos2B+cos2C,即2cos
2A=2cos(B+C)cos(B-C),即2cos
2A=-2cosAcos(B-C),
∴cosA=0或-cos(B-C)=cosA,
∴A=90°或A-B+C=180°(A-B+C=180°显然不可能,舍去),
则三角形为直角三角形.
点评:此题考查了正弦、余弦定理,以及三角形形状的判断,熟练掌握定理是解本题的关键.



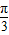 )
)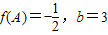 ,sin(A+C)=
,sin(A+C)= sinC,求△ABC的面积.
sinC,求△ABC的面积.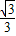 +1,0<α<
+1,0<α<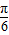 ,求sin2α的值.
,求sin2α的值.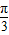 )
)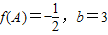 ,sin(A+C)=
,sin(A+C)= sinC,求△ABC的面积.
sinC,求△ABC的面积.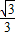 +1,0<α<
+1,0<α<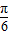 ,求sin2α的值.
,求sin2α的值. )
)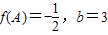 ,sin(A+C)=
,sin(A+C)= sinC,求△ABC的面积.
sinC,求△ABC的面积.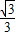 +1,0<α<
+1,0<α<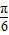 ,求sin2α的值.
,求sin2α的值.