
科目:高中数学 来源: 题型:
 如图,已知E、F为平面上的两个定点|EF|=6,|FG|=10,且2
如图,已知E、F为平面上的两个定点|EF|=6,|FG|=10,且2| EH |
| EG |
| HP |
| GE |
| 9 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
|
|
查看答案和解析>>
科目:高中数学 来源:2013届江西省高一下学期期中考试数学试题 题型:填空题
已知球O半径为1,A、B、C三点都在球面上,且每两点间的球面距离均为,则球心O到平面ABC的距离为 .
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省聊城市某重点中学高二(上)第四次模块检测数学试卷(理科)(解析版) 题型:解答题
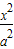 +
+ =1(a>b>0),点P的坐标为(-a,b).
=1(a>b>0),点P的坐标为(-a,b).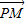 =
= (
( +
+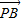 ),求点M的坐标;
),求点M的坐标; ,证明:E为CD的中点;
,证明:E为CD的中点;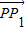 +
+ =
=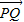 ,写出求作点P1、P2的步骤,并求出使P1、P2存在的θ的取值范围.
,写出求作点P1、P2的步骤,并求出使P1、P2存在的θ的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com