
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,+∞] | B. | (-∞,1] | C. | (-∞,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | 5 | C. | $\sqrt{31}$ | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?x≤0{,_{\;}}{2^x}≥3$ | B. | $?x≤0{,_{\;}}{2^x}<3$ | C. | $?x>0{,_{\;}}{2^x}≤3$ | D. | $?x>0{,_{\;}}{2^x}<3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
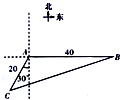 如图,位于A处的海面观测站获悉,在其正东方向相距40海里的B处有一艘渔船遇险,并在原地等待营救.在A处南偏西30°且相距20海里的C处有一艘救援船,该船接到观测站通告后立即前往B处求助,则sin∠ACB=$\frac{\sqrt{21}}{7}$.
如图,位于A处的海面观测站获悉,在其正东方向相距40海里的B处有一艘渔船遇险,并在原地等待营救.在A处南偏西30°且相距20海里的C处有一艘救援船,该船接到观测站通告后立即前往B处求助,则sin∠ACB=$\frac{\sqrt{21}}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
下列四个命题中错误的个数是( )
①垂直于同一条直线的两条直线相互平行;
②垂直于同一个平面的两条直线相互平行;
③垂直于同一条直线的两个平面相互平行;
④垂直于同一个平面的两个平面相互平行.
A.1 B.2 C.3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com