B
分析:根据函数的解析式,分类讨论,当x≤0时,f(x)=x+cosx,求导,判断导数的符号,确定函数的单调性,根据f(0)=1>0,x→-∞时,f(x)→-∞,从而求得函数零点的个数;当x>0时,f(x)=
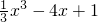
,求导,判断导数的符号,确定函数的单调性和极值,根据f(2)=
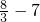
<0,f(0)=1>0,x→+∞时,f(x)→+∞,从而求得函数零点的个数.
解答:当x≤0时,f(x)=x+cosx,
f′(x)=1-sinx≥0,
∴f(x)在(-∞,0)上单调递增,且f(0)=1>0,x→-∞时,f(x)→-∞,
∴f(x)在(-∞,0)上有一个零点;
当x>0时,f(x)=
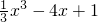
,
f′(x)=x
2-4=0,
解得x=2或x=-2(舍),
∴当0<x<2时,f′(x)<0,当x>2时,f′(x)>0,
∴f(x)在(0,2)上单调递减,在(2,+∞)上单调递增,
且f(2)=
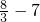
<0,f(0)=1>0,x→+∞时,f(x)→+∞,
∴f(x)在(0,+∞)上有两个零点;
综上函数f(x)=
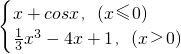
的零点个数为3个,
故选B.
点评:此题考查了函数零点问题,函数的零点个数问题实际上就是函数图象与x轴的交点个数问题,体现了转化的思想,利用导数研究函数的单调性和极值,从而确定函数的零点个数等基础题,同时考查了知识的灵活运用和运算能力.

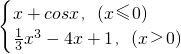 的零点个数为
的零点个数为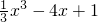 ,求导,判断导数的符号,确定函数的单调性和极值,根据f(2)=
,求导,判断导数的符号,确定函数的单调性和极值,根据f(2)=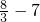 <0,f(0)=1>0,x→+∞时,f(x)→+∞,从而求得函数零点的个数.
<0,f(0)=1>0,x→+∞时,f(x)→+∞,从而求得函数零点的个数.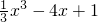 ,
,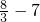 <0,f(0)=1>0,x→+∞时,f(x)→+∞,
<0,f(0)=1>0,x→+∞时,f(x)→+∞,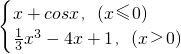 的零点个数为3个,
的零点个数为3个,
