对数列{an},规定{Van}为数列{an}的一阶差分数列,其中Van=an+1-an(n∈N*).对正整数k,规定{Vkan}为{an}的k阶差分数列,其中Vkan=Vk-1an+1-Vk-1an=V(VK-1an)(规定V0an=an).
(Ⅰ)已知数列{an}的通项公式an=n2+n(n∈N*),是判断{Van}是否为等差数列,并说明理由;
(Ⅱ)若数列{an}的首项a1=1,且满足V2an-Van+1+an=-2n(n∈N*),求数列{an}的通项公式.
解:(Ⅰ)△a
n=a
n+1-a
n=(n+1)
2+(n+1)-(n
2+n)=2n+2 …(4分)
则△a
n+1-△a
n=2,
所以△a
n是首项为4,公差为2的等差数列.…(6分)
(Ⅱ)△
2a
n-△a
n+1+a
n=-2
n,即△a
n+1-△a
n-△a
n+1+a
n=-2
n而△a
n=a
n+1-a
n,所以a
n+1-2a
n=2
n,∴
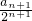
-

=

,(6分)
∴数列{

}构成以

为首项,

为公差的等差数列,
即

=

?a
n=n•2
n-1.(7分)
分析:(Ⅰ)根据题意:△a
n=a
n+1-a
n=(n+1)
2+(n+1)-(n
2+n)=2n+2,所以△a
n+1-△a
n=2.由此能够判断{△a
n}是等差数列.
(Ⅱ)由△
2a
n-△a
n+1+a
n=-2
n,知△a
n+1-△a
n-△a
n+1+a
n=-2
n,所以△a
n-a
n=2
n.由此入手能够求出数列{a
n}的通项公式.
点评:本题以新定义为载体,第(Ⅰ)题考查等差数列的判断,解题时要注意等差数列性质的合理运用;第(Ⅱ)题考查数列通项公式的求解方法,解题时要注意构造法的合理运用.

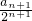 -
- =
= ,(6分)
,(6分) }构成以
}构成以  为首项,
为首项, 为公差的等差数列,
为公差的等差数列, =
= ?an=n•2n-1.(7分)
?an=n•2n-1.(7分)
