Question

已知x,y ,且x+2y≥1,则二次函数式u=x²+y²+4x-2y的最小值______.        

Answer 1

解析:

因为x,y ,且x+2y≥1,所以表示的平面区域如下图所示：

 函数式u=x²+y²+4x-2y=(x+2)²+(y-1)²-5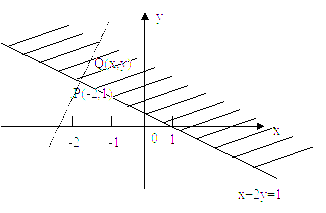，当x=-2,y=1时，即取P（-2，1）时，u的值为 最小，

但是点P（-2，1）不在区域x+2y≥1内，所以函数u=x²+y²+4x-2y不在点P处取得最小值。但是，当整体V=(x+2)²+(y-1)²取得最小值时，u就取得最小值，即取最小值。 可以理解为在区域x+2y≥1上任取一点Q（x,y）到点P（-2，1）的 距离的最小值，故作直线PQ垂直于直线：x+2y=1,垂足为Q就是要求的符合条件的点。

又L_PQ：2X-Y+5=0, 由  得点Q的坐标为Q（

  把Q（代入u=x²+y²+4x-2y=(x+2)²+(y-1)²-5=（

 即为所求的最小值