
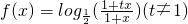 是奇函数.
是奇函数.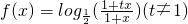 是奇函数,可得f(-x)+f(x)=0,可得(t2-1)x2=0,该式对定义域内的x恒成立,
是奇函数,可得f(-x)+f(x)=0,可得(t2-1)x2=0,该式对定义域内的x恒成立, =
= ,函数y=-1+
,函数y=-1+ 在(-1,1)上是减函数,
在(-1,1)上是减函数, ,解得:
,解得: .…
.… =
= ,函数y=-1+
,函数y=-1+ 在(-1,1)上是减函数,再由复合函数的单调性判断可知f(x)在区间(-1,1)上单调性.
在(-1,1)上是减函数,再由复合函数的单调性判断可知f(x)在区间(-1,1)上单调性. ,由此解得a的范围.
,由此解得a的范围.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
| 5π |
| 6 |
| 4π |
| 21 |
| π |
| 2 |
| π |
| 3 |
| 4π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:大连市第23中2009-2010学年度高二下学期期中考试(文科) 题型:单选题
对于定义在R上的函数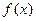 ,有下述四个命题,其中正确命题为( )
,有下述四个命题,其中正确命题为( )
①若函数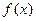 是奇函数,则
是奇函数,则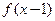 的图象关于点A(1,0)对称;
的图象关于点A(1,0)对称;
②若对x∈R,有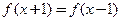 ,则
,则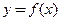 的图象关于直线
的图象关于直线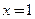 对称;
对称;
③若函数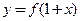 为偶函数,则
为偶函数,则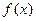 的图象关于直线
的图象关于直线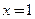 对称;
对称;
④函数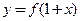 与函数
与函数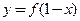 的图象关于直线
的图象关于直线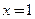 对称。
对称。
A. ①②④ B. ①③④ C. ②④ D. ①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com