
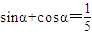 ,则α在第一或四象限;②函数y=sinx+cosx,
,则α在第一或四象限;②函数y=sinx+cosx,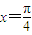 是它的一条对称轴,
是它的一条对称轴, 是它的一个对称中心;③函数
是它的一个对称中心;③函数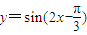 在
在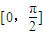 内是单调增函数;④把
内是单调增函数;④把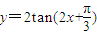 的图象向右平移
的图象向右平移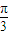 个单位可得到y=2tan2x的图象;⑤在△ABC中,cos2A>cos2B是A<B的充要条件.
个单位可得到y=2tan2x的图象;⑤在△ABC中,cos2A>cos2B是A<B的充要条件.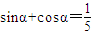 两边平方后,我们易求出sinα•cosα,由其符号可判断α所在的象限;将
两边平方后,我们易求出sinα•cosα,由其符号可判断α所在的象限;将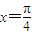 ,
,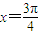 分别代入函数y=sinx+cosx,根据其值是否为函数的最值,易判断
分别代入函数y=sinx+cosx,根据其值是否为函数的最值,易判断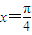 是否是它的一条对称轴,根据其值是否为0,可判断
是否是它的一条对称轴,根据其值是否为0,可判断 是否是它的一个对称中心;利用三角函数的单调性,可判断③的真假;根据函数平移变换法则,可判断④的对错;由倍角公式及正弦定理,我们也可得到⑤的正误.进行得到结论.
是否是它的一个对称中心;利用三角函数的单调性,可判断③的真假;根据函数平移变换法则,可判断④的对错;由倍角公式及正弦定理,我们也可得到⑤的正误.进行得到结论. ⇒
⇒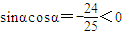 ,∴α在第二或四象限,错误.
,∴α在第二或四象限,错误. ,
, 时,
时,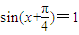 ,∴
,∴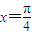 是它的一条对称轴,
是它的一条对称轴, 时,
时,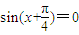 ,∴
,∴ 是它的一个对称中心,正确.
是它的一个对称中心,正确.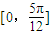 内
内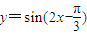 单增,在
单增,在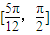 单减,∴错误.
单减,∴错误.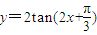 的图象向右平移
的图象向右平移 个单位得到
个单位得到 ≠2tan2x,∴错误.
≠2tan2x,∴错误.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com