练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （08年福州质检二）（12分）

    三个人进行某项射击活动，在一次射击中甲、乙、丙三人射中目标的概率分别为、、.

    （Ⅰ）一次射击后，三人都射中目标的概率是多少？

    （Ⅱ）用随机变量表示三个人在一次射击后射中目标的次数与没有射中目标的次数之差的绝对值，求随机变量的分布列及数学期望.

    解析：（I）一次射击后，三人射中目标分别记为事件A1，A2，A3，

    由题意知A1，A2，A3互相独立，且,…………2分

    .…………4分

    ∴一次射击后，三人都射中目标的概率是.…………5分

    （Ⅱ）证明：一次射击后，射中目标的次数可能取值为0、1、2、3，相应的没有射中目标的的次数可能取值为3、2、1、0，所以可能取值为1、3, …………6分

    则）+

     ………8分

    ∴，………10分

    ∴＝.………12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年福州质检二文）（12分）

    数列的前项和为，满足关系： .

     (Ⅰ)求的通项公式：

     (Ⅱ)设数列的前项和为，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年福州质检二）（12分）

    已知点A（－2,0），B（2,0），动点P满足：∠APB=2,且|PA||PB|sin2θ=2，

    （Ⅰ）求证：动点P的轨迹Q是双曲线；

    （Ⅱ）过点B的直线与轨迹Q交于两点M，N.试问轴上是否存在定点C，使为常数，若存在，求出点C的坐标；若不存在，说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年福州质检二）（12分）

    数列的前项和为，满足关系： .

    (Ⅰ)求的通项公式：

    (Ⅱ)设计算.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年福州质检二）（12分）

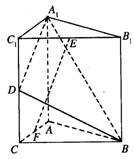
    如图，直三棱柱A1B1C1―ABC中，C1C=CB=CA=2，AC⊥CB. D、E分别为棱C1C、B1C1的中点.

        （Ⅰ）求与平面A1C1CA所成角的大小；

        （Ⅱ）求二面角B―A1D―A的大小；

        （Ⅲ）试在线段AC上确定一点F，使得EF⊥平面A1BD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年福州质检二）（12分）

    已知函数=2acos2x+bsinxcosx，且f(0)=，f()=.

    （Ⅰ）求的解析式；

    （Ⅱ）求的单调递增区间；

    （Ⅲ）函数的图象经过怎样的平移可使其对应的函数成为奇函数？

    查看答案和解析>>

    同步练习册答案