练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在中，角，，所对边分别为，，，且，，面积，则       ．


              

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知，则的值为   　　　 　　　   ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若，则“”是“方程表示双曲线”的（    ）

       A．充分不必要条件　    　　　Ｂ．必要不充分条件　　　　  

     C．充要条件　　　    　       D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列函数在其定义域上既是奇函数又是减函数的（   ）

    A．       B．       C．       D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个车间为了规定工时定额，需要确定加工零件所花费

    的时间，为此进行了次试验，收集数据如下：

    实验顺序

    第一次

    第二次

    第三次

    第四次

    第五次

    零件数（个）

    加工时间（分钟）

    在次试验中任取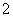次，记加工时间分别为，，求事件“，均小于分钟”的概率；

    请根据第二次，第三次，第四次试验的数据，求出关于的线性回归方程；

    根据得到的线性回归方程预测加工个零件所需要的时间．

    （线性回归方程中系数计算公式，．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    交通管理部门为了了解机动车驾驶员（简称驾驶员）对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查．假设四个社区驾驶员的总人数为，其中甲社区有驾驶员．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为，，，，则这四个社区驾驶员的总人数是（   ）

    A．               B．               C．               D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知实数，满足约束条件，则的最小值是（   ）

    A．                B．                C．                D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数与时刻(时)的关系为,其中是与气象有关的参数,且,若用每天的最大值为当天的综合放射性污染指数,并记作.

    (1)令,,求t的取值范围;

    (2)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标?

    查看答案和解析>>

    同步练习册答案