

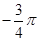
 kπ+
kπ+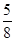 π],k∈Z,
π],k∈Z, ,可知2×
,可知2× +φ使f(x)取最值,即
+φ使f(x)取最值,即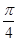 +φ=kπ+
+φ=kπ+ .(k∈Z),从而可求φ;由sinx的单增区间可求f(x)=sin(2x+φ)的单增区间.由|f′(x)|=|2cos(2x+φ)|≤2,直线5x-2y+c=0的斜率为
.(k∈Z),从而可求φ;由sinx的单增区间可求f(x)=sin(2x+φ)的单增区间.由|f′(x)|=|2cos(2x+φ)|≤2,直线5x-2y+c=0的斜率为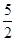 >2说明直线和f(x)的图象不能相切.
>2说明直线和f(x)的图象不能相切. 是函数y=f(x)的图像的对称轴,
是函数y=f(x)的图像的对称轴, +φ)=±1, 则有
+φ)=±1, 则有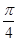 +φ=kπ+
+φ=kπ+ ,k∈Z.
,k∈Z. 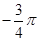
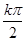 +
+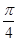 ,k∈Z.
,k∈Z.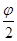 得到,
得到,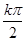 +
+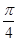 -
-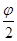 =
= k∈Z.
k∈Z.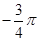 .
. 是函数y=f(x)的图像的对称轴. 所以f(
是函数y=f(x)的图像的对称轴. 所以f( -x)=f(
-x)=f( +x).
+x). -x)+φ]=sin[2(
-x)+φ]=sin[2( +x)+φ],
+x)+φ], -x)+φ=2kπ+2(
-x)+φ=2kπ+2( +x)+φ(舍去),
+x)+φ(舍去), -x)+φ]+[2(
-x)+φ]+[2( +x)+φ]=2kπ+π.
+x)+φ]=2kπ+π. 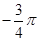
 π,因此y=sin(2x-
π,因此y=sin(2x- π),
π),  ≤2x-
≤2x- π≤2kπ+
π≤2kπ+ ,(k∈Z),
,(k∈Z), π)的单调增区间为[kπ+
π)的单调增区间为[kπ+ kπ+
kπ+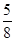 π],k∈Z,
π],k∈Z, π)≥0可得,2kπ-
π)≥0可得,2kπ- ≤2x-
≤2x- π≤2kπ+
π≤2kπ+ k∈Z,
k∈Z, π)的单调增区间为[kπ+
π)的单调增区间为[kπ+ ,kπ+
,kπ+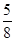 π] k∈Z,
π] k∈Z, π)]′|=|2cos(2x-
π)]′|=|2cos(2x- π)|≤2,
π)|≤2,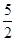 >2,
>2, π)的图象不相切.
π)的图象不相切. π)-
π)-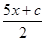 ,
,  π)-
π)-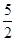 ,
, π)≤1,F′(x)≠0.
π)≤1,F′(x)≠0.  π)的图像不相切.
π)的图像不相切.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com