C
分析:由f(x)=x
-1=

是奇函数,故排除A. 由f(x)=cosx 在(0,+∞)上没有单调性,故排除B. 由f(x)=log
2|x|在区间(0,+∞)上是单调递增的函数,故排除D.
经检验只有C满足条件.
解答:由于函数f(x)=x
-1=

是奇函数,故排除A.
由于函数f(x)=cosx 在(0,+∞)上没有单调性,故排除B.
由于函数f(x)=
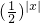
是偶函数,在区间(0,+∞)上f(x)=

单调递减,故C满足条件.
由于函数 f(x)=log
2|x|在区间(0,+∞)上是单调递增的函数,故排除D.
故选C.
点评:本题主要考查函数的奇偶性、单调性的判断,属于中档题.

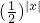
 阅读快车系列答案
阅读快车系列答案