
 上的点,又点F1(-4,0),F2(4,0),下列结论正确的是( )
上的点,又点F1(-4,0),F2(4,0),下列结论正确的是( )科目:高中数学 来源: 题型:
 某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系.
某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源:江苏省南通市通州区2012届高三4月查漏补缺专项检测数学试题 题型:044
如图1,OA、OB是某地一个湖泊的两条互相垂直的湖堤,线段CD和曲线段EF分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥CD上某点P分别修建与OA、OB平行的栈桥PM、PN,且以PM、PN为边建一个跨越水面的三角形观光平台PMN.建立如图2所示的直角坐标系,测得线段CD的方程是x+2y=20(x≤x≤20),曲线段EF的方程是xy=200(4≤x≤50),设点P的坐标为(x,y),记z=xy(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度).


(1)求z的取值范围;
(2)试写出三角形观光平台PMN面积S△PMN关于z的函数解析式,并求出该面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
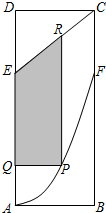 某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系.
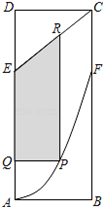
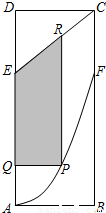
某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源:江苏期中题 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省盐城中学高二(上)期中数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com