
【题目】已知 ![]() 为常数),
为常数), ![]() ,且当x1 , x2∈[1,4]时,总有f(x1)≤g(x2),则实数a的取值范围是 .
,且当x1 , x2∈[1,4]时,总有f(x1)≤g(x2),则实数a的取值范围是 .
【答案】![]()
【解析】解:依题意知,当x1 , x2∈[1,4]时,f(x1)max≤g(x2)min , 由“对勾'函数单调性知, ![]() =2x+
=2x+ ![]() =2(x+
=2(x+ ![]() )在区间[1,4]上单调递增,
)在区间[1,4]上单调递增,
∴g(x2)min=g(1)=3;
∵ ![]() =2ax2+2x,
=2ax2+2x,
当a=0时,f(x)=2x在区间[1,4]上单调递增,∴f(x)max=f(4)=8≤3不成立,故a≠0;
∴f(x)=2ax2+2x为二次函数,其对称轴方程为:x=﹣ ![]() ,
,
当a>0时,f(x)在区间[1,4]上单调递增,f(x)max=f(4)=8≤3不成立,故a>0不成立;
当a<0时,
1°若﹣ ![]() ≤1,即a≤﹣
≤1,即a≤﹣ ![]() 时,f(x)在区间[1,4]上单调递减,
时,f(x)在区间[1,4]上单调递减,
f(x)max=f(1)=2a+2≤3恒成立,即a≤﹣ ![]() 时满足题意;
时满足题意;
2°若1<﹣ ![]() <4,即﹣
<4,即﹣ ![]() <a<﹣
<a<﹣ ![]() 时,f(x)max=f(﹣
时,f(x)max=f(﹣ ![]() )=﹣
)=﹣ ![]() ≤3,解得:﹣
≤3,解得:﹣ ![]() <a≤﹣
<a≤﹣ ![]() ;
;
3°若﹣ ![]() ≥4,即﹣
≥4,即﹣ ![]() ≤a<0时,f(x)在区间[1,4]上单调递增,
≤a<0时,f(x)在区间[1,4]上单调递增,
f(x)max=f(4)=32a+8≤3,解得a≤﹣ ![]() (﹣
(﹣ ![]() ,0),故不成立,
,0),故不成立,
综合1°2°3°知,实数a的取值范围是:(﹣∞,﹣ ![]() ].
].
所以答案是: ![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( ) ①命题“x∈R,x3﹣x2+1≤0”的否定是“ ![]() ;
;
②“ ![]() ”是“三个数a,b,c成等比数列”的充要条件;
”是“三个数a,b,c成等比数列”的充要条件;
③“m=﹣1”是“直线mx+(2m﹣1)y+1=0和直线3x+my+2=0垂直”的充要条件:
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,P(x,y)为函数y=1+lnx图象上一点,记直线OP的斜率k=f(x). (Ⅰ)若函数f(x)在区间(m,m+ ![]() )(m>0)上存在极值,求实数m的取值范围;
)(m>0)上存在极值,求实数m的取值范围;
(Ⅱ)当x≥1时,不等式f(x)≥ ![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在y轴上的椭圆E的中心是原点O,离心率等于 ![]() ,以椭圆E的长轴和短轴为对角线的四边形的周长为4
,以椭圆E的长轴和短轴为对角线的四边形的周长为4 ![]() ,直线,l:y=kx+m与y轴交干点P,与椭圆E相交于A、B两个点. (Ⅰ)求椭圆E的方程;
,直线,l:y=kx+m与y轴交干点P,与椭圆E相交于A、B两个点. (Ⅰ)求椭圆E的方程;
(Ⅱ)若 ![]() =3
=3 ![]() ,求m2的取值范围.
,求m2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足bn=an+1﹣an(n=1,2,3,…).
(1)若bn=10﹣n,求a16﹣a5的值;
(2)若 ![]() 且a1=1,则数列{a2n+1}中第几项最小?请说明理由;
且a1=1,则数列{a2n+1}中第几项最小?请说明理由;
(3)若cn=an+2an+1(n=1,2,3,…),求证:“数列{an}为等差数列”的充分必要条件是“数列{cn}为等差数列且bn≤bn+1(n=1,2,3,…)”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AAl , A1B1上,且AE= ![]() ,A1F=
,A1F= ![]() ,CE⊥EF,M为AB中点 (Ⅰ)证明:EF⊥平面CME;
,CE⊥EF,M为AB中点 (Ⅰ)证明:EF⊥平面CME;
(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.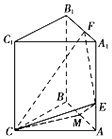
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法中,
①命题“存在x∈R,x2﹣x>0”的否定是“对于任意x∈R,x2﹣x<0”;
②命题“p且q为真”是“p或q为真”的必要不充分条件;
③已知幂函数f(x)=xα的图象经过点(2, ![]() ),则f(4)的值等于
),则f(4)的值等于 ![]() ;
;
④已知向量 ![]() =(3,﹣4),
=(3,﹣4), ![]() =(2,1),则向量
=(2,1),则向量 ![]() 在向量
在向量 ![]() 方向上的投影是
方向上的投影是 ![]() .
.
说法错误的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了苏俄生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的数学和物理成绩,如表:
成绩 编号 | 1 | 2 | 3 | 4 | 5 |
物理(x) | 90 | 85 | 74 | 68 | 63 |
数学(y) | 130 | 125 | 110 | 95 | 90 |
(1)求数学成绩y对物理成绩x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() (
( ![]() 精确到0.1).若某位学生的物理成绩为80分,预测他的数学成绩;
精确到0.1).若某位学生的物理成绩为80分,预测他的数学成绩;
(2)要从抽取的这五位学生中随机选出2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率.(参考公式: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() ) (参考数据:902+852+742+682+632=29394,90××125+74×110+68×95+63×90=42595)
) (参考数据:902+852+742+682+632=29394,90××125+74×110+68×95+63×90=42595)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com