
 +
+ =1(a>b>0)的一个焦点坐标为(
=1(a>b>0)的一个焦点坐标为( ,0),短轴一顶点与两焦点连线夹角为120°.
,0),短轴一顶点与两焦点连线夹角为120°.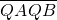 ≤4,求m的取值范围.
≤4,求m的取值范围.解:(1)由题意知a=2b,c= ,a2=b2+c2
,a2=b2+c2
解得a=2,b=1,∴椭圆方程为 +y2=1
+y2=1
(2)由(1)可知A(-2,0),设B点坐标为(x1,y1),
直线l的方程为y=k(x+2)
于是A、B两点的坐标满足方程组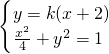
由方程消去y并整理得:(1+4k2)x2+16k2x+16k2-4=0
由-2x1=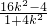 得x1=
得x1=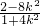 ,从而y1=
,从而y1=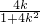
设线段AB的中点为M,则M的坐标为(-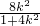 ,
, )
)
以下分两种情况:
①当k=0时,点B的坐标为(2,0),线段AB的垂直平分线为y轴,
于是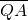 =(-2,-m),
=(-2,-m),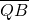 =(2,-m),
=(2,-m),
由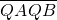 ≤4
≤4
得:-2 ≤m≤2
≤m≤2
②当k≠0时,线段AB的垂直平分线方程为
y- =-
=- (x+
(x+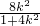 )
)
令x=0,得m=-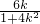
由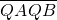 =-2x1-m(y1-m)
=-2x1-m(y1-m)
=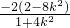 +
+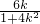 (
(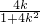 +
+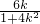 )
)
=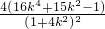 ≤4
≤4
解得-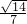 ≤k≤
≤k≤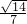 且k≠0
且k≠0
∴m=-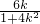 =-
=-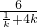
∴当-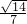 ≤k<0时,
≤k<0时, +4k≤-4
+4k≤-4
当0<k≤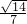 时,
时, +4k≥4
+4k≥4
∴- ≤m≤
≤m≤ ,且m≠0
,且m≠0
综上所述,- ≤m≤
≤m≤ ,且m≠0
,且m≠0
 ,a2=b2+c2,由此能得到椭圆方程.
,a2=b2+c2,由此能得到椭圆方程.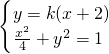 ,由方程消去y并整理得:(1+4k2)x2+16k2x+16k2-4=0,由-2x1=
,由方程消去y并整理得:(1+4k2)x2+16k2x+16k2-4=0,由-2x1=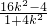 得x1=
得x1=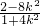 ,从而y1=
,从而y1=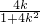 ,设线段AB的中点为M,则M的坐标为(-
,设线段AB的中点为M,则M的坐标为(-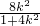 ,
, .然后再分类讨论进行求解.
.然后再分类讨论进行求解.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:2009-2010学年湖北省武汉市六校高三(上)第一次联考数学试卷(文科)(解析版) 题型:填空题
 +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 .查看答案和解析>>
科目:高中数学 来源:2012年安徽省合肥八中高考数学一模试卷(理科)(解析版) 题型:解答题
 +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则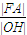 的最大值为 .
的最大值为 .查看答案和解析>>
科目:高中数学 来源:2012年安徽省合肥八中高考数学一模试卷(文科)(解析版) 题型:解答题
 +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 .查看答案和解析>>
科目:高中数学 来源:2010年河南省高二上学期12月份考试数学卷(文理) 题型:选择题
已知椭圆 =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若 (应为PB),则离心率为
(应为PB),则离心率为
A、 B、
B、 C、
C、 D、
D、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com