练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知首项为的等比数列的前n项和为, 且成等差数列.

    (Ⅰ) 求数列的通项公式;

    (Ⅱ) 证明.

     

    【答案】

    (Ⅰ) 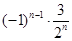 (Ⅱ)见解析

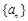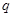    【解析】(Ⅰ)设等比数列的公比为，因为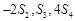成等差数列，所以

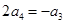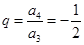    S4 + 2S2 =4S4 – S3，即，于是，又=，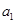

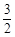    所以等比数列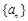的通项公式为=.

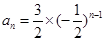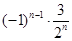    (Ⅱ)由(Ⅰ)得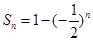，所以=，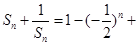

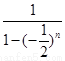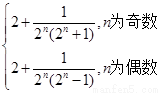    当n为奇数时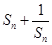，随n的增大而减小，所以=；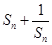

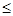
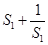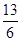    当n为偶数时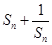，随n的增大而增大，所以=，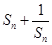

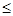
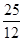    故对于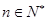，有.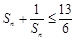

    本题第（Ⅰ）问，由S3 + a3, S5 + a5, S4 + a4成等差数列可以求出公比，进而由等比数列的通项公式求出结果；第(Ⅱ)问，先求出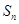，然后分n为奇数与偶数讨论得出数列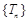的最大项与最小项的值.对第（Ⅰ）问，要注意细心计算；第二问，注意分n为奇数与偶数两种情况讨论.

    【考点定位】本小题主要考查等差数列的概念，等比数列的概念、通项公式、前n项和公式，数列的基本性质等基础知识，考查分类讨论的思想，考查运算能力、分析问题和解决问题的能力.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年四川绵阳高中高三第二次诊断性考试理科数学试卷（解析版） 题型：解答题

    已知首项为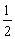的等比数列{an}是递减数列，其前n项和为Sn，且S1+a1，S2+a2，S3+a3成等差数列．

    （Ⅰ）求数列{an}的通项公式；

    （Ⅱ）若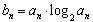，数列{bn}的前n项和Tn，求满足不等式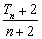≥的最大n值．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年四川绵阳高中高三第二次诊断性考试文科数学试卷（解析版） 题型：解答题

    已知首项为的等比数列{an}是递减数列，其前n项和为Sn，且S1+a1，S2+a2，S3+a3成等差数列．

    （Ⅰ）求数列{an}的通项公式；

    （Ⅱ）已知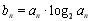，求数列{bn}的前n项和．

     

    查看答案和解析>>

    科目：高中数学 来源：2013年天津市高考数学试卷（理科）（解析版） 题型：解答题

    已知首项为的等比数列{an}不是递减数列，其前n项和为Sn（n∈N*），且S3+a3，S5+a5，S4+a4成等差数列．
    （Ⅰ）求数列{an}的通项公式；
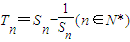    （Ⅱ）设，求数列{Tn}的最大项的值与最小项的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知首项为的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.

    (1)求数列{an}的通项公式.

    (2)证明Sn+≤(n∈N*).

    查看答案和解析>>

    同步练习册答案