
 已知椭圆
已知椭圆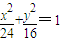 ,直线
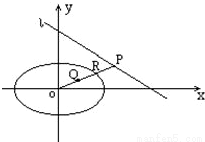
,直线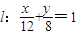 .P是l上点,射线OP交椭圆于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,当点P在l上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线.
.P是l上点,射线OP交椭圆于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,当点P在l上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线. 解:由题设知点Q不在原点.设P、R、Q的坐标分别为(xP,yP),(xR,yR),(x,y),其中x,y不同时为零.
解:由题设知点Q不在原点.设P、R、Q的坐标分别为(xP,yP),(xR,yR),(x,y),其中x,y不同时为零.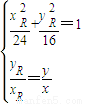
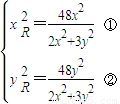
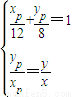 .
.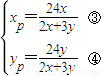
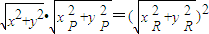

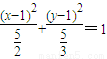 (其中x,y不同时为零).
(其中x,y不同时为零). 和
和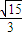 且长轴与x轴平行的椭圆、去掉坐标原点.
且长轴与x轴平行的椭圆、去掉坐标原点.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:044
已知椭圆![]() ,直线
,直线![]() .P是l上点,射线OP交椭圆于点R,又点Q在OP上且满足|OQ|·|OP|=|OR|2,当点P在l上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线.
.P是l上点,射线OP交椭圆于点R,又点Q在OP上且满足|OQ|·|OP|=|OR|2,当点P在l上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:高中数学 来源:1995年全国统一高考数学试卷(理科)(解析版) 题型:解答题
 已知椭圆
已知椭圆 ,直线
,直线 .P是l上点,射线OP交椭圆于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,当点P在l上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线.
.P是l上点,射线OP交椭圆于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,当点P在l上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线.查看答案和解析>>
科目:高中数学 来源:1995年全国统一高考数学试卷(文科)(解析版) 题型:解答题
 已知椭圆
已知椭圆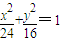 ,直线
,直线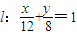 .P是l上点,射线OP交椭圆于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,当点P在l上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线.
.P是l上点,射线OP交椭圆于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,当点P在l上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com