
已知函数f(n)= 且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
(A)-100 (B)100 (C)-1020 (D)1020
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
已知定义在R上的函数f(x)=ax(0<a<1),且f(1)+f(-1)= ,若数列{f(n)}(n∈N*)的前n项和等于
,若数列{f(n)}(n∈N*)的前n项和等于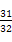 ,则n等于( )
,则n等于( )
(A)4 (B)5 (C)6 (D)7
查看答案和解析>>
科目:高中数学 来源: 题型:
某林场年初有森林木材存量S m3,木材以每年25%的增长率生长,而每年年末要砍伐固定的木材量为x m3,为实现经过两次砍伐后的木材存量增加50%,则x的值为( )
(A)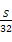 (B)
(B)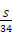 (C)
(C)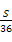 (D)
(D)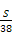
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}满足a1+3a2+32a3+…+3n-1an=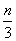 ,n∈N*.
,n∈N*.
(1)证明:数列{an}为等比数列;
(2)设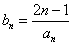 ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com