
若数列![]() 满足
满足![]() (
(![]() 为正常数;
为正常数;![]() ),则称
),则称![]() 为“等方比数列”.
为“等方比数列”.
甲:数列![]() 是等方比数列; 乙:数列
是等方比数列; 乙:数列![]() 是等比数列,则
是等比数列,则
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
若数列![]() 满足:
满足:![]() 是常数),则称数列
是常数),则称数列![]() 为二阶线性递推数列,且定义方程
为二阶线性递推数列,且定义方程![]() 为数列
为数列![]() 的特征方程,方程的根称为特征根; 数列
的特征方程,方程的根称为特征根; 数列![]() 的通项公式
的通项公式![]() 均可用特征根求得:
均可用特征根求得:
①若方程![]() 有两相异实根
有两相异实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
②若方程![]() 有两相同实根
有两相同实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
再利用![]() 可求得
可求得![]() ,进而求得
,进而求得![]() .
.
根据上述结论求下列问题:
(1)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(2)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(3)当![]() ,
,![]() (
(![]() )时,记
)时,记![]() ,若
,若![]() 能被数
能被数![]() 整除,求所有满足条件的正整数
整除,求所有满足条件的正整数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分18分,第(1)小题6分,第(2)小题6分,第(3)小题6分)
若数列![]() 满足:
满足:![]() 是常数),则称数列
是常数),则称数列![]() 为二阶线性递推数列,且定义方程
为二阶线性递推数列,且定义方程![]() 为数列
为数列![]() 的特征方程,方程的根称为特征根; 数列
的特征方程,方程的根称为特征根; 数列![]() 的通项公式
的通项公式![]() 均可用特征根求得:
均可用特征根求得:
①若方程![]() 有两相异实根
有两相异实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
②若方程![]() 有两相同实根
有两相同实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
再利用![]() 可求得
可求得![]() ,进而求得
,进而求得![]() .
.
根据上述结论求下列问题:
(1)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(2)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(3)当![]() ,
,![]() (
(![]() )时,记
)时,记![]() ,若
,若![]() 能被数
能被数![]() 整除,求所有满足条件的正整数
整除,求所有满足条件的正整数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省佛山市高三教学质量检测(一)文科数学 题型:解答题
设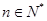 ,圆
,圆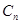 :
: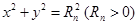 与
与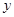 轴正半轴的交点为
轴正半轴的交点为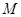 ,与曲线
,与曲线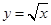 的交点为
的交点为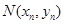 ,直线
,直线 与
与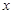 轴的交点为
轴的交点为 .
.
(1)用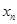 表示
表示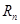 和
和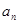 ;
;
(2)若数列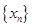 满足:
满足: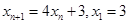 .
.
①求常数 的值使数列
的值使数列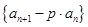 成等比数列;
成等比数列;
②比较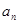 与
与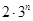 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
若数列![]() 满足
满足![]() (
(![]() 为正常数;
为正常数;![]() ),则称
),则称![]() 为“等方比数列”.
为“等方比数列”.
甲:数列![]() 是等方比数列; 乙:数列
是等方比数列; 乙:数列![]() 是等比数列,则
是等比数列,则
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com