
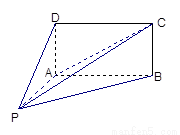
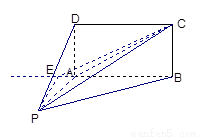
如图,四棱锥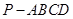 的底面
的底面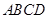 为矩形,且
为矩形,且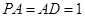 ,
,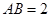 ,
, ,
,
(Ⅰ)求证:平面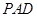
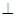 平面
平面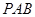 ;
;
(Ⅱ)求直线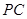 与平面
与平面 所成角的正弦值
所成角的正弦值
(I)证明:由题意得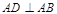 且
且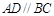
又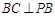 ,则
,则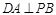 ……………………………3分
……………………………3分
则 平面
平面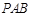 , 故平面
, 故平面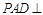 平面
平面 ………………6分
………………6分
(Ⅱ)解法1:

以点A为坐标原点,AB所在的直线为y轴建立空间直角坐标系如右图示,则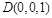 ,
,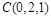 ,
,
可得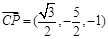 , ……………………………8分
, ……………………………8分
平面ABCD的单位法向量为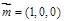 ,………10分
,………10分
设直线PC与平面ABCD所成角为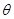 ,则
,则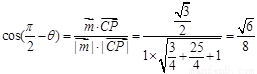 …13分
…13分
则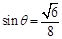 ,即直线PC与平面ABCD所成角的正弦值
,即直线PC与平面ABCD所成角的正弦值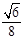 …………………………………14分
…………………………………14分
解法2:
由(I)知 平面
平面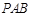 ,∵
,∵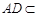 面
面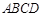
∴平面ABCD⊥平面PAB,
在平面PAB内,过点P作PE⊥AB,垂足为E,则PE⊥平面ABCD,连结EC,则∠PCE为直线PC与平面ABCD所成的角,在Rt△PEA中,∵∠PAE=60°,PA=1,∴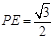 ,又
,又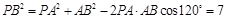 ∴
∴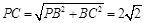
在Rt△PEC中 .
.
【解析】略


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(本小题满分12分)
 如图,四棱锥
如图,四棱锥![]() 的底面为正方形,侧棱
的底面为正方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,
,![]() 分别是线段
分别是线段![]() 的中点.
的中点.
(Ⅰ)求证:![]() //平面
//平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南长沙重点中学高三上学期第四次月考文科数学试卷(解析版) 题型:解答题
如图,四棱锥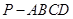 的底面
的底面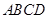 为矩形,且
为矩形,且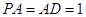 ,
,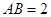 ,
,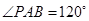 ,
,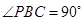 ,
,
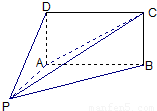
(Ⅰ)平面PAD与平面PAB是否垂直?并说明理由;
(Ⅱ)求直线PC与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省六校联合体高三第二次联考数学理卷 题型:解答题
(本小题满分14分)
如图,四棱锥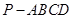 的底面
的底面 为菱形,
为菱形,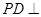 平面
平面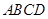 ,
,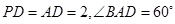 ,
,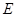 、
、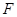 分别为
分别为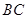 、
、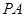 的中点。
的中点。
(I)求证: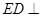 平面
平面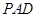 ;
;
 (Ⅱ)求三棱锥
(Ⅱ)求三棱锥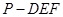 的体积;
的体积;
(Ⅲ)求平面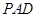 与平面
与平面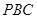 所成的锐二面角大小的余弦值。
所成的锐二面角大小的余弦值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com