
 ,点
,点 、
、 在函数
在函数 的图象上,
的图象上, 在函数
在函数 的图象上,设
的图象上,设
 .
. 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 项和为
项和为 ;
; ,记数列
,记数列 的前
的前 项和为
项和为 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小.
的大小. 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 吨,此时所需生产费用为(
吨,此时所需生产费用为( )万元,当出售这种商品时,每吨价格为
)万元,当出售这种商品时,每吨价格为 万元,这里
万元,这里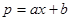 (
( 为常数,
为常数, )
) 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 从点
从点 出发,分别按逆时针方向沿周长均为
出发,分别按逆时针方向沿周长均为 的正三角形、正方形运动一周,
的正三角形、正方形运动一周, 两点连线的距离
两点连线的距离 与点
与点 走过的路程
走过的路程 的函数关系分别记为
的函数关系分别记为 ,定义函数
,定义函数 对于函数
对于函数 ,下列结论正确的个数是( )
,下列结论正确的个数是( )
 ;
; 的图像关于直线
的图像关于直线 对称;
对称; 值域为
值域为 ;
; 在区间
在区间 上单调递增.
上单调递增.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 (正常情况
(正常情况 ,且教职工平均月评价分数在50分左右,若有突出贡献可以高于100分)计算当月绩效工资
,且教职工平均月评价分数在50分左右,若有突出贡献可以高于100分)计算当月绩效工资 元.要求绩效工资不低于500元,不设上限且让大部分教职工绩效工资在600元左右,另外绩效工资越低、越高人数要越少.则下列函数最符合要求的是( )
元.要求绩效工资不低于500元,不设上限且让大部分教职工绩效工资在600元左右,另外绩效工资越低、越高人数要越少.则下列函数最符合要求的是( )A. | B. |
C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com