
 如图,已知抛物线y2=2px(p>0)有一个内接直角三角形,直角顶点在原点,两直角边OA与OB的长分别为1和8,求抛物线方程.
如图,已知抛物线y2=2px(p>0)有一个内接直角三角形,直角顶点在原点,两直角边OA与OB的长分别为1和8,求抛物线方程.| 1 |
| k |
| 1 |
| k |
|
| 2p |
| k2 |
| 2p |
| k2 |
| 2p |
| k |
| 2p |
| k2 |
| 2p |
| k |
| k2+1 |
| k4 |
| ② |
| ① |
| 4 |
| 5 |
2
| ||
| 5 |
4
| ||
| 5 |


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
| 按家庭人均月收入分组(百元) | 第一组[10,16) | 第二组[16,22) | 第三组[22,28) | 第四组[28,34) | 第五组[34,40) | 第六组[40,46] |
| 频率 | 0.1 | 0.2 | 0.15 | a | 0.1 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
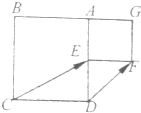 如图,已知正方形ABCD的边长为2,点E为边AD的中点,以AE为边向外作正方形AEFG,现将正方形AEFG绕点A按顺时针方向转动至AE与AB重合,则
如图,已知正方形ABCD的边长为2,点E为边AD的中点,以AE为边向外作正方形AEFG,现将正方形AEFG绕点A按顺时针方向转动至AE与AB重合,则| CE |
| DF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x |
| A、命题“p或q”是假命题 |
| B、命题“(¬p)且q”是真命题 |
| C、命题“p或(¬q)”是真命题 |
| D、命题“(¬p)且(¬q)”是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com